Mit einem Roboter ein Labyrinth lösen

Einführung

Neben dem Linienfolger ist das Lösen eines Labyrinths eine beliebte Aufgabe für mobile Roboter. Labyrinthe gibt es in vielen verschiedenen Formen und Größen. Die im Folgenden beschriebenen Ansätze und Ideen beziehen sich alle auf Labyrinthe, bei denen die Pfade mit einer schwarzen Linie auf weißem Grund dargestellt sind und Abzweigungen immer im 90 Grad Winkel erfolgen.

Im Wesentlichen kann das Lösen eines Labyrinths in vier unterschiedliche Teilaufgaben unterteilt werden:

1. Der Roboter muss einer Linie folgen können.
2. Der Roboter muss die unterschiedlichen Kreuzungen erkennen.
3. Der Roboter muss an einer Kreuzung zu jeden beliebigen Weg abbiegen können.
4. Der Roboter benötigt Regeln (z.B. Rechte-Hand-Regel), wie er das Ende des Labyrinths finden soll.

Im Folgenden wird auf die Realisierung der Punkte 2 bis 4 eingegangen. Algorithmen für einen Linienfolger wurden an anderer Stelle besprochen und werden hier nicht weiter aufgeführt.

note

Auch wenn sich die folgenden Programmauszüge auf den Roboter Zumo 32u4 der Firma Pololu beziehen, sind die Erläuterungen sehr allgemeiner Natur und sollten sich problemlos auf andere Roboter übertragen lassen.

Unterschiedliche Kreuzungstypen erkennen

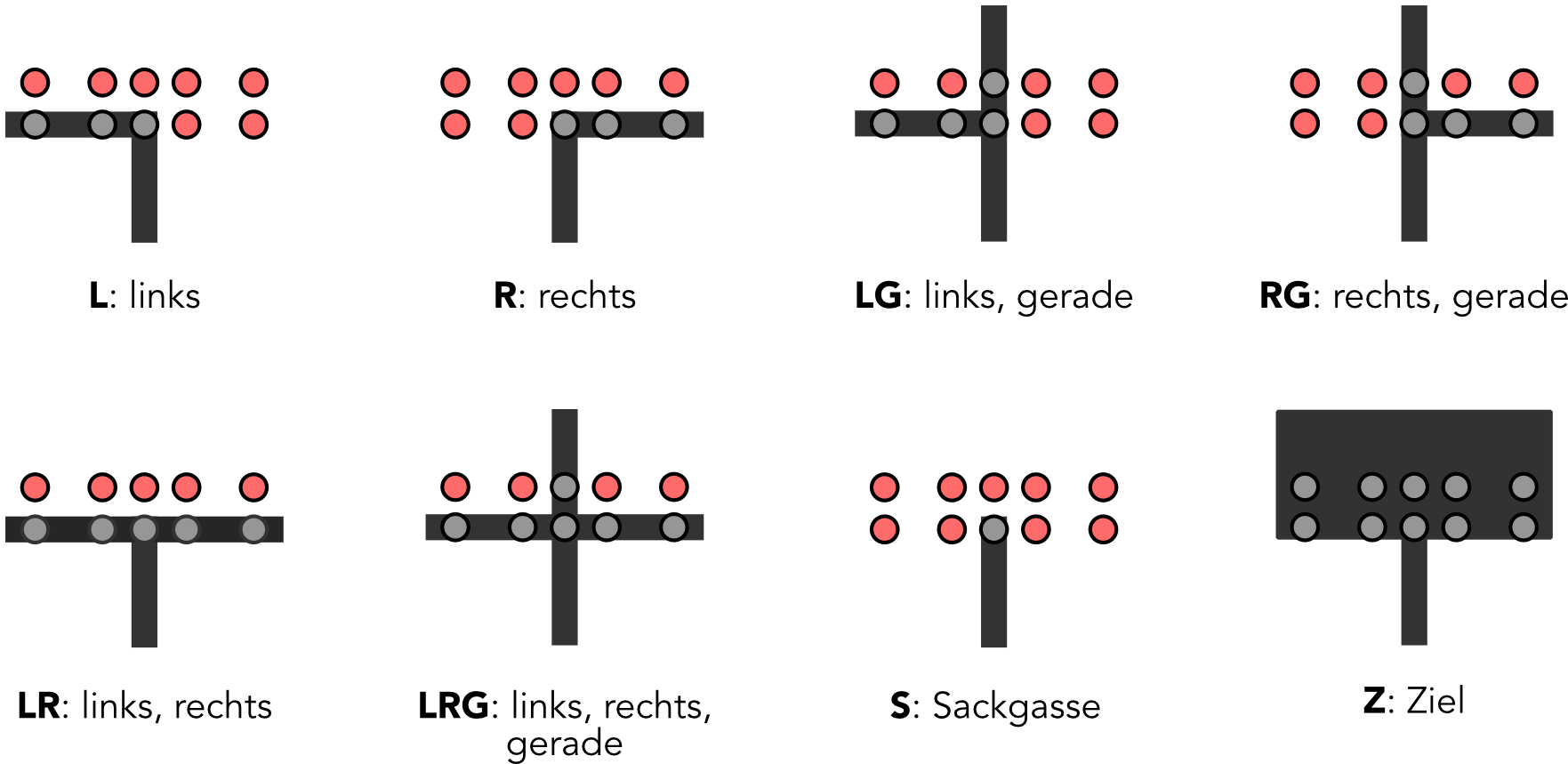
Die Kreuzungserkennung des Roboters soll alle Kreuzungen (Abzweigungen, Sackgassen, Ziel) des Labyrinths erkennen. Insgesamt gibt es 8 unterschiedliche Kreuzungstypen, die mit den Bodensensoren erkannt werden können. Wie in der Abbildung dargestellt, wird jedem Kreuzungstyp eine Abkürzung (L, R, LG, RG, etc.) zugewiesen, welche später zum Lösen des Labyrinths benötigt werden.

Aufzählungsdatentyp enum für die Kreuzungstypen

Ähnlich wie bei den endlichen Automaten, macht es auch bei den Kreuzungstypen Sinn, einen eigenen Datentyp (KreuzungsTyp) für die verschiedenen Kreuzungen zu erstellen.

// Deklaration eines neuen Datentyps `KreuzungsTyp`
enum KreuzungsTyp {L, R, LR, LG, RG, LRG, S, ZIEL};

Damit lässt sich dann eine Variable vom erstellten Datentyp KreuzungsTyp deklarieren und ihr zum Beispiel den Wert LRG für eine Kreuzung mit 4 Abzweigungen zuweisen:

KreuzungsTyp kreuzung = LRG;  // Variable `kreuzung` vom Typ `KreuzungsTyp`

Außerdem kann eine Funktion bestimmenKreuzung() definiert werden, deren Rückgabewert vom Typ KreuzungsTyp ist:

// Funktion mit Rückgabewert vom Typ `KreuzungsTyp`
KreuzungsTyp bestimmenKreuzung(){  
    // ...
}

Dadurch lässt sich die gesamte Kreuzungserkennung in einer Funktion bestimmenKreuzung() durchführen und das Ergebnis wird als Datentyp KreuzungsTyp zurückgegeben. Das vollständige Programm zum Lösen des Labyrinths wird damit deutlich lesbarer und strukturierter.

Bestimmen des Kreuzungstypes

Das Bestimmen der Kreuzungstypen für einen Roboter, dessen Bodensensoren auf einer Linie angeordnet sind (z.B. Zumo 32u4) erfolgt in drei Schritten:

1. Der Roboter folgt so lange der Linie, bis einer der äußeren Sensoren eine Abzweigung erkennt (Welche Bedingung muss für eine Sackgasse erfüllt sein?)
2. Anschließend sollte der Roboter bis auf die Mitte der Linie fahren. Dort wird erneut auf Abzweigungen überprüft. So wird sicher gestellt, dass alle Abzweigungen erkannt werden, auch wenn der Roboter nicht ganz senkrecht auf die Abzweigungen trifft.
3. Im nächsten Schritt fährt der Roboter über die Linie hinweg. Für das später folgende Abbiegen ist es am besten, wenn er genau mittig auf der Kreuzung stehen bleibt. Nun kann der Roboter überprüfen, ob es auch einen zusätzlichen Weg geradeaus gibt oder ob das Ziel (Ende des Labyrinths) erreicht wurde.

Der 1. Schritt wird mit der Funktion fahrenZurKreuzung() und der 2. und 3. Schritt mit der Funktion bestimmenKreuzung() realisiert.

Funktion fahrenZurKreuzung()

Die Funktion fahrenZurKreuzung() soll den Roboter solange der Linie folgen lassen, bis ein Bodensensor den Beginn einer Kreuzung erkennt (1. Schritt). Wurde der Beginn einer Kreuzung erkannt, wird anschließend die Funktion bestimmenKreuzung() zum Ermitteln des Kreuzungstypes aufgerufen (2. und 3. Schritt).

// Folgt der Linie bis zur nächsten Kreuzung und 
// gibt den erkannten Kreuzungstyp zurück.
KreuzungsTyp fahrenZurKreuzung() {
  bool kreuzung = false;

  // der Linie folgen, bis eine Kreuzung erkannt wurde
  while (!kreuzung) { 
    folgenLinie();

    // Bedingung für eine Kreuzung (oder Sackgasse), 
    // wenn alle Sensoren auf einer Linie sind (z.B. Zumo).
    // Sind die Bodensensoren auf einem Kreisbogen angeordnet (3pi+),
    // gibt es eine bessere Bedingung ..
    kreuzung = aufLinie(0) || aufLinie(4) || !aufLinie(2);
  }
  
  motors.setSpeeds(0,0); // stoppen bei Kreuzung ...
  // ... und `bestimmenKreuzung()` aufrufen und das Ergebnis zurückgeben.
  return bestimmenKreuzung(); 
}

Die Funktion folgenLinie() realisiert den Algorithmus zum Linienfolgen mit einem geeignetem Algorithmus.

aufLinie()

Die in fahrenZurKreuzung() verwendete Funktion bool aufLinie(byte pSensor) gibt true zurück, wenn sich der angegebene Bodensensor über einer schwarzen Linie befindet und false, wenn der Sensor keine Linie erkannt hat.

// Die Funktion aktualisiert NICHT die Sensorwerte. 
// Zum Auslesen der Sensoren die Funktion readCalibrated() aufrufen.
bool aufLinie(byte pSensor) {
  const int schwelleLinie = 100;                    // Schwellert zum Erkennen einer Abzweigung
  return lineSensorValues[pSensor] > schwelleLinie; // globaler Array `lineSensorValues[]`
}

tip

Zum Erkennen einer Kreuzung sollte ein möglichst kleiner Schwellwert für die Sensoren verwendet werden (z.B. 100). Ist der Schwellwert zu groß, wird der Algorithmus zum Linienfolgen zu lange ausgeführt und führt so zu einer ungenauen Positionierung des Roboters an der Kreuzung (der Roboter würde leicht schräg an der Kreuzung stehen).

Funktion bestimmenKreuzung()

Der 2. und 3. Schritt für die Bestimmung des Kreuzungstypes soll mit der Funktion bestimmenKreuzung() umgesetzt werden. Ohne die fertige Funktion bestimmenKreuzung() zu präsentieren, sollen an dieser Stelle ein paar Hinweise zur möglichen Realisierung gegeben werden.

Die Hauptaufgabe der Funktion bestimmenKreuzung() ist das Erkennen der Kreuzungstypen. Deshalb sollte die Funktion vom Typ KreuzungsTyp sein und am Ende den ermittelten Kreuzungstyp zurückgegeben.

Das Erkennen des Kreuzungstyps wird wie oben beschrieben umgesetzt. Da sich die verschiedenen Kreuzungstypen aber aus unterschiedlichen Kombinationen von erkannten Abzweigungen ergibt, werden die boolschen Variablen lLinks, lRechts und lGerade genutzt, um zuerst die erkannten Abzweigungen zu speichern.

Anschließend wird der sich ergebende Kreuzungstyp bestimmt und als Wert vom Typ KreuzungsTyp (also L, R, LG, RG, etc.) von der Funktion zurückgegeben.

Damit der Roboter die Kreuzungen zuverlässig erkennt, sollte für die Positionierung auf der Linie (2. Schritt) und der Positionierung mittig auf der Kreuzung (3. Schritt) der Motorencoder verwendet werden. Eine einfache Positionierung mit einer Zeitsteuerung kann gelegentlich funktionieren, stellt aber eine sehr fehleranfällige Lösung dar.

// Bestimmen des Kreuzungstypes. 
// Die Funktion sollte aufgerufen werden, sobald ein Sensor
// etwas anderes als der zu folgenden Linie erkennt.
KreuzungsTyp bestimmenKreuzung(){
    // An der Kreuzung erkannte Abzweigungen (0: keine Abzweigung)
    bool lLinks  = 0;   // Abzweigung links 
    bool lRechts = 0;   // Abzweigungs rechts
    bool lGerade = 0;   // Weg gereadeaus
    
    /*
    Die Funktion wird aufgerufen, wenn bereits ein Sensor einen Abzweig erkannt hat.
        1. Die Sensoren auf die Mitte der Linie positionieren (Motorencoder verwenden!).
        2. Sensorwerte einlesen.
        3. Abzweigungen bestimmten und `lLinks`/`lRechts` entsprechend setzen.
        4. Weiterfahren, bis der Roboter mittig auf der Kreuzung steht.
        5. Sensorwerte einlesen
        6. `lGerade` setzen und auf Ziel überprüfen
    */

    // Funktion gibt mit `return` den ermittelten KreuzungsTyp zurück
    if (/* Abzweigung links */){
        return L;
    }
    else if (/* Abzweigung rechts */){
        return R;
    }
    else if (/* Abzweigung links, gerade*/){
        return LG;
    }
    /* usw. */
}

fahrenStreckeMM()

Außerdem wird die Funktion fahrenStreckeMM() benötigt, welche den Roboter mit Hilfe der Radencoder eine exakte Strecke zurücklegen lässt. Dadurch wird die exakte Positionierung des Roboters auf der Kreuzung vereinfacht.

#define MM_PRO_IMPULS 0.128  // Encoderauflösung (Zumo 32u4 Standard)

void fahrenStreckeMM(int pSpeed, int pStreckeMM){
  long encoderImpulse = pStreckeMM / MM_PRO_IMPULS;
  
  // Zu programmierende Eigenschaft:
  // Fahre solange geradeaus, wie die mittlere Anzahl
  // beider Motorenencoder kleiner als `encoderImpulse` ist
  // ... 
}

Aufgaben

Schreiben Sie eine Funktion KreuzungsTyp fahrenZurKreuzung(), welche den Roboter einer Linie entlang bis zu einer Kreuzung folgt, den Kreuzungstyp der Linie bestimmt (es sollen alle Typen erkannt werden) und stoppt. Der Rückgabewert der Funktion ist der ermittelte Kreuzungstyp.

Verwenden Sie die selbstgeschriebene Funktion KreuzungsTyp fahrenZurKreuzung(), um mit dem Roboter beliebige Kreuzungstypen zu erkennen und auf dem Display ausgeben zu lassen. Nachdem eine Kreuzung erkannt wurde, folgt der Roboter auf Knopfdruck erneut der Linie bis zur nächsten Kreuzung. Bei dieser Aufgabe soll der Roboter noch keine Funktion zum Abbiegen an Kreuzungen implementiert haben (folgt später).

Abbiegen an Kreuzungen

Das Abbiegen an Kreuzungen wurde bereits an anderes Stelle besprochen. An dieser Stelle soll aber darauf hingewiesen werden, dass das Drehen zum Abzweig nur mit einer zeitlichen Verzögerung (delay()) nicht besonders sicher funktioniert. Deutlich genauer ist es, wenn sich der Roboter solange dreht, bis der mittlere Bodensensor die abzweigende Linie erkannt hat. Bei einer breiten Linie sollte ein Schwellwert von ca. 900 recht gut funktionieren.

#define LEFT 1
#define RIGHT 2
void abbiegenKreuzung(int pRichtung){
    if (pRichtung == LEFT){        // gegen den Uhrzeigersinn 
        // Drehen, bis der Roboter mittig auf der Linie steht.
        // Unbedingt Bodensensoren zum Erkennen der Linie nutzen.
    }
    else if (pRichtung == RIGHT){  // mit dem Uhrzeigersinn
        // Wie oben, nur andere Richtung ...
    }
}

Lösen des Labyrinths mit Rechter-Hand-Regel

Die Idee hinter der Rechten-Hand-Regel zum Lösen eines Labyrinths ist recht einfach: Berühre mit einer imaginären rechten Hand immer die rechte Wand. Gibt es zum Beispiel einen Abzweig nach rechts, fährt der Roboter auch nach rechts. Hat der Roboter eine Sackgasse erreicht, dreht er sich im 180 Grad und fährt dann wieder zurück. Auf diese Weise kann jedes Labyrinth mit außenliegendem Start und Zielort gelöst werden.

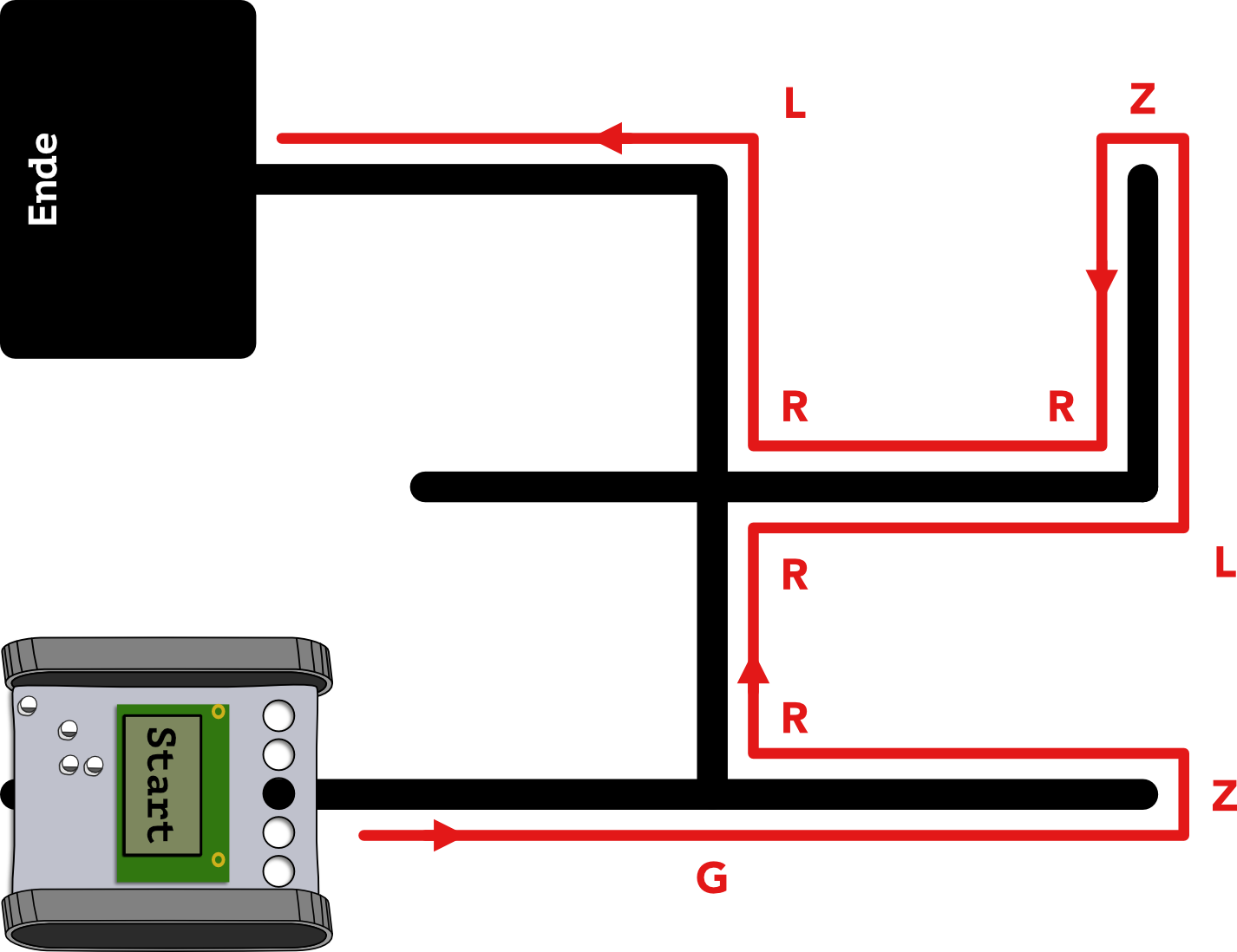
In der Abbildung ist der Weg des Roboters nach der Rechten-Hand-Regel dargestellt. Der zurückgelegt Weg kann auch als Abfolge von Aktionen (links L, rechts R, gerade G, Ende E) gespeichert werden. Im dargestellten Labyrinth ergibt sich mit der Rechten-Hand-Regel folgender Weg: GZRRLZRRLE

Ein Ansatz für die Implementierung einer Funktion fahrenMitRHR() könnte wie folgt aussehen:

void fahrenMitRHR(){               // RHR: Rechte-Hand-Regel
  bool end = false; 

  while (!end){                   // `end` sollte am Ziel auf true gesetzt werden
    KreuzungsTyp kreuzung;
    kreuzung = fahrenZurKreuzung();

    switch(kreuzung){
        case L:                    // nur Abzweig nach links  
          abbiegenKreuzung(LEFT);  // links abbiegen
          break;
        /*

        case-Anweisungen für alle anderen Kreuzungstypen

        */
    }
}

Eine Schleife (while(!end)) wird solange ausgeführt, wie der Roboter das Ende des Labyrinths noch nicht gefunden hat. Innerhalb der Schleife fährt der Roboter mit fahrenZurKreuzung() bis zur nächsten Kreuzung, ermittelt dort den Kreuzungstyp und biegt entsprechend der Rechten-Hand-Regel ab. Ist das Ende erreicht, wird der boolsche Ausdruck end auf true gesetzt und die Schleife und somit auch die Funktion fahrenMitRHR() beendet.

Aufgaben

1. Schreiben Sie ein Programm, welches den Roboter mit der Rechten-Hand-Regel von einem beliebigen Startort zum Ziel navigeren lässt. Am Ziel angekommen, soll der Roboter stehen bleiben.

2. Speichern Sie den zurückgelegten Weg in einem String. In dem String wird für jede Kreuzung die gewählte Fahrtrichtung L (links). R (rechts), G (gerade), Z (zurück), E (Ende) abgelegt. Geben Sie an jeder Kreuzung den aktuell zurückgelegten Fahrweg auf dem Display aus.

   Hinweis: Strings lassen sich einfach verknüpfen, bzw. verlängern:

   String einString = ""; // Instanziiert einen leeren String
   Serial.println(test);  // (keine Ausgabe)
   
   einString += 'L';
   Serial.println(test);  // Ausgabe: L
   
   einString += 'R';
   einString += 'G';
   Serial.println(test); // Ausgabe: LRG

   In der Arduino Referenz finden sie eine Auflistung aller Methoden der String Klasse.

Optimierung der Rechten-Hand-Regel

Auch wenn der Roboter an dieser Stelle in der Lage sein sollte ein Labyrinth zu lösen, so ist der gewählt Weg nicht unbedingt besonders kurz. Sackgassen erkennt der Roboter erst, wenn er sie erreicht hat und macht daher unnötige Umwege.

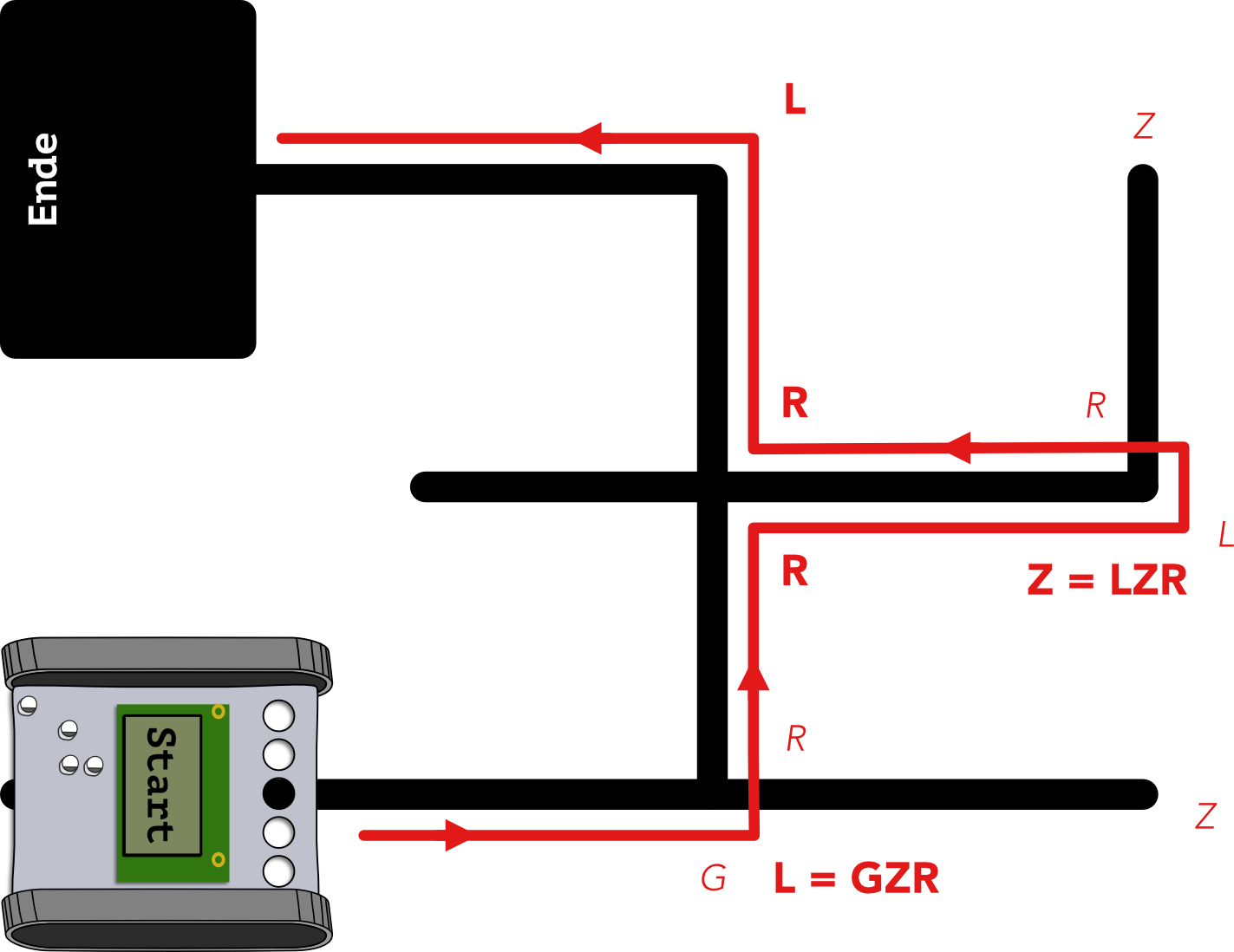
Betrachtet man die einzelnen Sackgassen, wird klar, dass der Roboter auch vorher abbiegen kann. Die zuerst angefahrende Sackgasse kann er abkürzen, indem er sofort nach links L fährt und nicht erst den langen Weg gerade G, zurück Z und rechts R fährt. Aus dem Weg GZR wird somit L. Ähnlich verhält es sich mit der zweiten Sackgasse. Hier kann der Weg LZR zu Z vereinfacht werden.

In dem nun teilweise verkürzten Weg gibt es jedoch immer noch eine Sackgasse, welche der Roboter abkürzen kann. Hier führt der Weg RZR zu der Abkürzung L

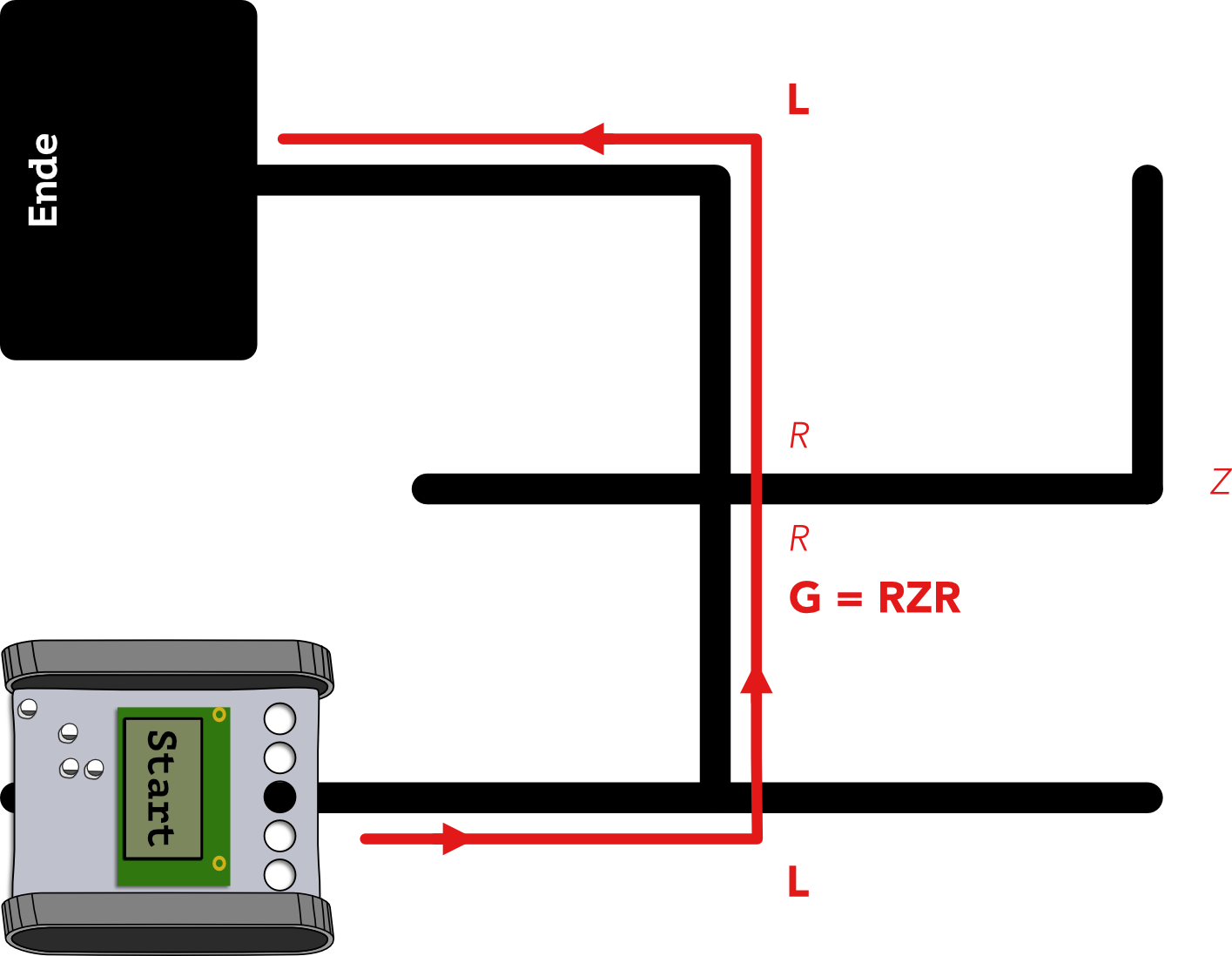
Aus den beiden Abbildungen ergibt sich somit eine noch unvollständige Liste von Regeln zum Vereinfachen des Weges:

• L = GZR
• Z = LZR
• G = RZR

Das Anwenden der Regeln auf den ursprünglichen Weg kann auf zwei Arten geschehen:

• Beim ersten Ansatz wird gewartet, bis der gesamte Weg mit der Rechten-Hand-Regel bestimmt wurde und anschließend solange nach zu ersetzenden Muster gesucht, bis sich der Weg nicht weiter vereinfachen lässt.
• Beim zweiten Ansatz werden nach jeder neu durchgeführten Aktion die letzten drei Aktionen auf ein zu ersetzendes Muster untersucht.

Vereinfachen nachdem der Weg bestimmt wurde

GZRRLZRRLE       (ursprünglicher Weg)
GZR R LZR RLE    (zwei Sackgassen GZR und LZR)
  L  R  Z  RLE   (die beiden `Z` werde ersetzt,GZR = L, LZR = Z)
LRZRLE           (es entsteht ein neuer Pfad)
L RZR LE         (eine Sackgasse RZR)
L  G  LE         (neues `Z` ersetzen, RZR = G) 
LGLE             (maximal gekürzter Weg)

Vereinfachen während der Weg bestimmt wird

G       (1. Kreuzung: G)
GZ      (2. Kreuzung: Z)
GZR     (3. Kreuzung: R)
L       (ersetzen GZR = L)
LR      (4. Kreuzung: R)
LRL     (5. Kreuzung: L)
LRLZ    (6. Kreuzung: Z)
LRLZR   (7. Kreuzung: R)
LRZ     (ersetzen LZR = Z)
LRZR    (8. Kreuzung: R)
LG      (ersetzen RZR = G)
LGL     (9. Kreuzung: L)
LGLE    (10. Kreuzung: E -> Maximal gekürzter Weg)

Aufgaben

1. Analysieren Sie die Teilwege GZG, RZG, RZL und leiten Sie für jeden eine Vereinfachung mit nur einer Roboteraktion (L,R,G oder Z) ab. Zeichnen Sie zu jedem Teilweg die zugehörige Wegskizze.

2. Notieren Sie sich für die beiden abgebildeten Labyrinthe den ungekürzten Weg nach der Rechten-Hand-Regel. Schreiben Sie anschließend ein Programm, welches den Weg so weit wie möglich kürzt. (Testen Sie Ihr Programm zuerst ohne Roboter.)

   

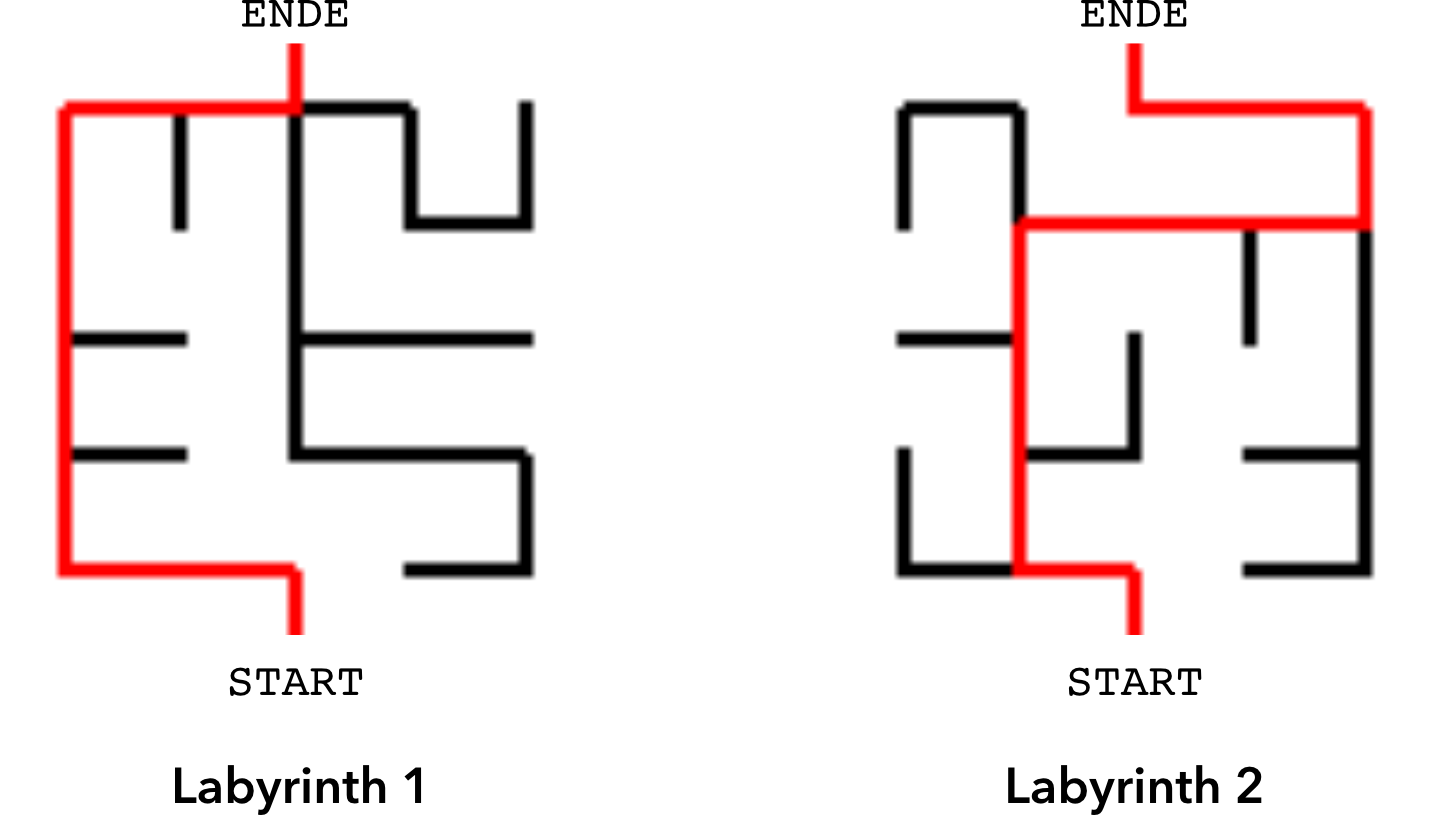
   Hinweis: Die String-Methode einString.replace(s1,s2) ersetzt im String einString den Teilstring s1 durch den Teilstring s2. Link.

   Wokwi: Weg kürzen RHR

3. Lassen Sie den Roboter in zwei Läufen durch ein Labyrinth fahren. Bei der ersten Fahrt findet der Roboter mit der Rechten-Hand-Regel das Ziel und beim zweiten Lauf fährt er auf verkürztem Weg zum Ziel.

   Variation: Der Roboter fährt mit der Rechten-Hand-Regel vom Start zum Ziel, dreht dort um und fährt auf möglichst kurzem Weg zurück zum Start.

Trémaux-Algorithmus

Die Rechte-Hand-Regel ist einfach zu implementieren und findet in vielen Labyrinthen auch sicher das Ziel. Eine Einschränkung gibt es allerdings: Befindet sich der Start oder das Ziel im Inneren des Labyrinths und hat das Labyrinth Schleifen, so wird die Rechte-Hand-Regel nicht immer das Ziel finden.

Bei solchen Labyrinthen (und auch allen anderen) findet der Trémaux-Algorithmus, benannt nach dem Franzosen Charles Pierre Trémaux (1859–1882), sicher das Ziel. Beim Trèmaux-Algorithmus werden Markierungen verwendet, um bereits abgegangene Pfade zu markieren, und somit auch etwaige Schleifen zu erkennen.

Der Algorithmus

---

Beim Betreten und Verlassen wird der jeweilige Weg an der Kreuzung immer markiert. Ein Weg beginnt bzw. endet immer an einer Kreuzung. Ein Weg, der zweimal markiert ist, darf nicht erneut betreten werden.

An einer Kreuzung wird die erste mögliche Regel der folgenden Regel angewendet:

• Ist nur der aktuelle Ausgang (aktueller Weg) markiert, gehe beliebigen anderen Weg.
• Weitere Wege sind markiert, dann gehe zurück. Markiere den Eingang ein zweites Mal.
• Der Ausgang (aktueller Weg) ist 2 mal markiert, folge dem Weg mit den wenigsten Markierungen

Wurde mit dem Trémaux-Algorithmus das Ende des Labyrinths gefunden, ergibt sich der Weg zurück zum Ziel ganz einfach, indem nur dem Weg gefolgt wird, welcher nicht mit zwei Markierungen versperrt ist.

---

Links

• Maze Generator - Erzeugt fast beliebige Labyrinthe
• Maze Solving
• Maze Solving Robot
• Teaching a Robot to Solve a Line Maze
• Arduino findet durch Labyrinth
• Maze Generator with Processing - Tutorial