Zum Hauptinhalt springen

Drehbewegungen eines Roboters mit einem Gyroskop bestimmen

Gyroskop​

Ein Gyroskop, eigentlich Drehratensensor genannt, ist wie ein Beschleunigungssensor Teil einer inertialen Messeinheit (IMU - inertial measurement unit), mit welcher ohne äußere Bezugspunkte Änderungen der Lage und Postion eines Objektes bestimmt werden. Mit einer inertialen Messeinheit kann daher immer nur die Lage zu einem anfänglich bekannten Startpunkt bestimmt werden. Heutzutage finden sich solche Messeinheiten zur Bestimmung der Lage und Position in vielen elektronischen Geräten, wie zum Beispiel Smartphones oder Gimbals zur Stabilisierung von Kamerabildern.

Während Gyroskope früher ziemlich groß und sehr teuer waren, gibt es seit einiger Zeit so genannten mikroelektromechanische Systeme (MEMS), welche die Corioliskraft ausnutzen und Gyroskope wesentlich kleiner und preiswerter gemacht haben. Heutzutage werden Sie millionenfach in Form winziger integrierte Schaltung mit einer Kantenlänge von wenigen Millimetern verwendet.

Drehwinkel in der Ebene bestimmen​

Das vom Zumo 32U4 oder dem 3pi+ 32u4 verwendete Gyroskop kann Drehraten um drei verschieden Achsen (siehe Abbildung) messen. Soll bestimmt werden, ob sich der Roboter auf einer ebenen Fläche nach links oder rechts dreht (entspricht der xy-Ebene), so kann dafür die Drehrate um die z-Achse verwendet werden.

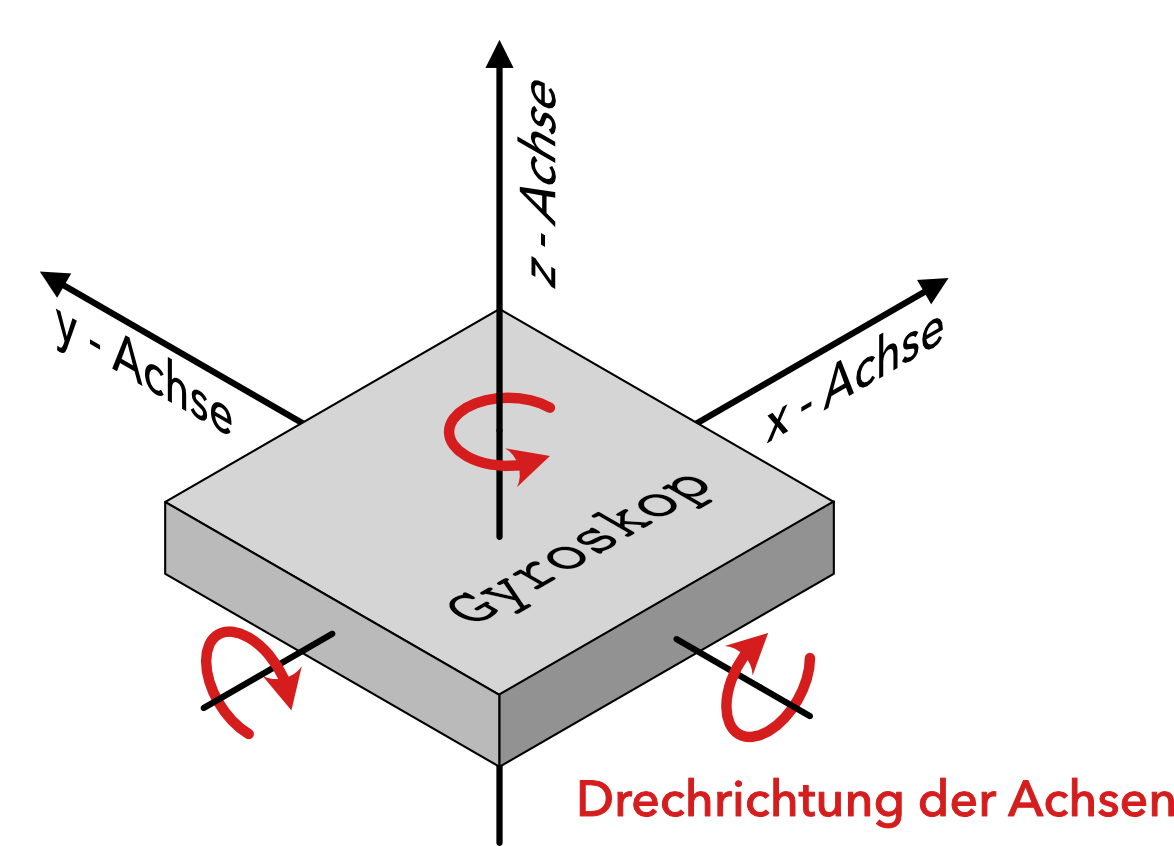
Drehwinkel eines Gyroskops

Mit einem Gyroskop wird in der Regel die Drehrate bzw. die Winkelgeschwindigkeit ω\omega und nicht die Orientierung oder der Drehwinkel gemessen. Dreht sich das Gyroskop in einer Sekunde einmal um sich selbst, würde eine Winkelgeschwindigkeit von 360 Grad/s gemessen werden.

Ähnlich wie die Integration der Geschwindigkeit die zurückgelegt Strecke ergibt, lässt sich auch der Drehwinkel φ\varphi aus der Integration der Winkelgeschwindigkeit ω\omega über die Zeit tt bestimmen:

φ=∫ω(t)  dt\varphi = \int \omega(t)\; \text{d}t

Der Mikrocontroller kann das Integral, ähnlich wie bei der Streifenmethode, als Summe vieler einzelner Winkeländerungen Δφi\Delta \varphi_i bestimmen.

∫0tω(τ)  dτ=∑i=0nΔφi=Δφ1+Δφ2+Δφ3+⋯+Δφn=φ(t)\begin{aligned} \int_0^{t} \omega(\tau)\; d{\tau} &= \sum_{i=0}^n \Delta\varphi_i \\ &= \Delta\varphi_1 + \Delta\varphi_2 +\Delta\varphi_3 + \cdots +\Delta\varphi_n \\ &= \varphi(t) \end{aligned}

Die einzelnen Winkeländerungen Δφi\Delta \varphi_i hängen natürlich von der momentanen Winkelgeschwindigkeit ωi\omega_i und dem Zeitintervall Δti\Delta t_i ab. Ist das Zeitintervall Δti\Delta t_i klein genug, bzw. ändert sich die Winkelgeschwindigkeit in dem Zeitintervall nur sehr wenig, so ergibt sich für die Änderung des Drehwinkels:

Δφi≈ωiΔti\Delta\varphi_i \approx \omega_i \Delta t_i

Diese Multiplikation kann dann sehr einfach mit dem Mikrocontroller realisiert werden:

dWinkel = drehRate * dt

Werden anschließend alle Winkeländerungen dWinkel aufaddiert, erhält man die aktuelle Änderung des Drehwinkels:

winkel = winkel + dWinkel

Leider ist die Praxis etwas komplizierter als die Theorie. Zum einen gibt des Gyroskop des Roboters die Winkelgeschwindigkeit nicht in Grad pro Sekunde aus und zum anderen führt ein reales, verrauschtes Signal der Winkelgeschwindigkeit aufgrund der durchzuführenden Integration schnell zu fehlerhaften Drehwinkeln. Wie mit dem Gyroskop trotzdem ein recht genauer Drehwinkel bestimmt werden kann, wird in dem folgenden Abschnitt erklärt.

Achtung

Das Gyroskop bestimmt die Drehrate (Winkelgeschwindigkeit) des Roboters, nicht aber die Änderung der Orientierung, bzw. den Drehwinkel.

Aufgaben

  1. Folgende Winkelgeschwindigkeiten (Drehgeschwindigkeiten) wurden gemessen:

    ω(t) = 180 Grad/s für 0s < t < 0,5s

    ω(t) = 0 Grad/s für 0,5s < t < 1s

    ω(t) = -200 Grad/s für 1s < t < 1,9s

    ω(t) = 0 Grad/s für 1,9s < t < 2,5s

    ω(t) = 150 Grad/s für 2,5s < t < 3,1s

    ω(t) = 0 Grad/s für 3,1s < t< 4s

    ω(t) = 80 Grad/s * t² für 4s < t < 7s

    Zeichnen Sie den Verlauf der Winkelgeschwindigkeit als Liniendiagramm in ein geeignetes Koordinatensystem.

    Bestimmen Sie rechnerisch den aktuellen Drehwinkel und tragen sie diesen in das selbe Koordinatensystem ein. Ergänzen sie die entsprechende Achsenbeschriftung.

Auslesen der Drehrate​

Das Gyroskop ist beim Zumo 32U4 über die so genannte I2C-Schnittstelle (sprich: I Quadrat C) mit dem Mikrocontroller des Roboters verbunden. Wie bei der seriellen Schnittstelle zur Kommunikation mit dem PC handelt es sich hier um einen seriellen Datenbus, der den bidirektionalen Austausch von Daten ermöglicht.

Das folgende Programm initialisiert die I2C-Schnittstelle für die Kommunikation mit dem Gyroskop und ließt die aktuelle Drehrate um die z-Achse (also in der xy-Ebene) aus.

// Drehrate um die z-Achse des Zumo 32U4 auslesen

#include <Wire.h>                 // I2C Bibliothek
#include <Zumo32U4.h>             // Zumo 32U4 Bibliothek

Zumo32U4IMU imu;                  // Objekt für Inertialsensoren (inkl. Gyroskop)

void setup() {
  Serial.begin(115200);
  Wire.begin();                   // Starten der I2C Verbindung
  imu.init();                     // Inertialsensoren (inkl. Gyroskop) initialisieren
  imu.configureForTurnSensing();  // Empfindlichkeit und Filter einstellen
}

void loop()
{
  imu.readGyro();                 // Auslesen der Gyro-Daten
  int drehRate = imu.g.z;         // Drehrate in z-Richtung (xy-Ebene)
  Serial.println(drehRate);        
  delay(50);
}

Damit die I2C-Schnittstelle zur Kommunikation mit dem Gyroskop überhaupt genutzt werden kann, muss mit

#include <Wire.h>                 // I2C Bibliothek

die Wire-Bibliothek für die I2C-Schnittstelle eingebunden werden. Nachdem das Objekt für die Inertialsensoren (inkl. dem Gyroskop) deklariert wurde

Zumo32U4IMU imu;                  // Objekt für Inertialsensoren (inkl. Gyroskop)

wird in der setup() Funktion die I2C-Schnittstelle gestartet und anschließend das Gyroskop (als Teil der Inertialsensoren) initialisiert und konfiguriert.

Wire.begin();                     // Starten der I2C Verbindung
imu.init();                       // Inertialsensoren (inkl. Gyroskop) initialisieren
imu.configureForTurnSensing();    // Empfindlichkeit und Filter einstellen

Ist die Konfiguration abgeschlossen, werden mit der Zeile

imu.readGyro();              // Auslesen der Gyro-Daten

die Drehraten des Gyroskops für die 3 Achsen (x,y,z) ausgelesen. Auf die einzelnen Werte kann dann über das Objekt imu mit imu.g.x, imu.g.y und imu.g.z zugegriffen werden:

int drehRate = imu.g.z       // Drehrate in z-Richtung (xy-Ebene)

Messen und Kalibrieren​

Die vom Gyroskop übermittelte Drehrate wird als Integer-Datentyp bereitgestellt und soll an dieser Stelle noch ohne Einheit betrachtet werden. (Die Umrechnung in Grad pro Sekunde erfolgt später). Bei einem ruhenden Roboter (ruhender Sensor) ergibt sich der folgende Verlauf der Drehrate (dunkle Linie).

Idealer Weise sollte für den Fall des ruhenden Roboters die Drehrate, also die Drehgeschwindigkeit immer null sein. Die realen Messwerte sind jedoch verrauscht und variieren daher. Außerdem weisen die Messwerte einen Mittelwert auf, der deutlich von null abweicht. Dieser Mittelwert der Drehrate eines ruhenden Sensors wird Offset-Fehler genannt.

Da der Offset-Fehler eine mittlere Drehrate vortäuscht, die der stehende Roboter nicht haben kann, sollte vor der Weiterverarbeitung der Drehrate der Offset-Fehler immer bestimmt und anschließend kompensiert werden.

Am einfachsten lässt sich der Offset-Fehler bestimmen, indem über eine feste Anzahl von Messwerten der Mittelwert bestimmt wird.

// Bestimmen des Offset-Fehlers (in void setup())
float sumGyro = 0;
for (int i = 0 ; i < 4000; i++) {
  while (!imu.gyroDataReady()){}    // Warten auf neue Gyro-Daten
  imu.readGyro();                   // Einlesen der Gyro-Daten
  sumGyro += imu.g.z;               // imu.g.z: Winkelgeschwindigkeit der z-Achse 
}
float offSet = sumGyro / 4000;      // Offset-Fehler als Fließkommazahl berechnen

Der so ermittelte Offsetfehler sollte anschließend von allen andern Messwerten abgezogen werden, damit die ermittelte Drehrate mittelwertfrei ist.

float drehRate = imu.g.z - offSet; // mittlwertfreier (aber verrauschter) Messwert des Gyroskops

Der Verlauf der kalibrierten Drehrate ist ebenfalls in dem obigen Abbildung dargestellt (helle Linie).

Aufgaben
  1. Erläutern Sie, was der Offset-Fehler eines Gyroskops ist und warum er bei der Weiterverarbeitung der Messdaten berücksichtigt werden muss.
  2. Wird ein ruhender Roboter von einem Benutzer hochgehoben, ändert sich aller Wahrscheinlichkeit nach auch die Orientierung des Roboters. Schreiben Sie ein Programm, dass die Orientierungsänderung überwacht und eine LED aufleuchten lässt, sobald der Roboter seine Orientierung ändert. Ist der Roboter wieder in Ruhe, soll die LED wieder ausgehen.

Bestimmen des Drehwinkels​

Umrechnung der Drehrate in Grad pro Sekunde​

Die vom Gyroskop gemessene Drehrate wurde bisher ohne Einheit betrachtet. Zum späteren Bestimmen des Drehwinkels ist es jedoch sinnvoll, die Drehrate in eine Winkelgeschwindigkeit mit der Einheit Grad pro Sekund (deg/s) umzurechnen. Der notwendige Umrechnungsfaktor hängt dabei von den Einstellungen des Gyroskops ab.

Die vom Zumo 32U4 verwendeten Gyroskope (es gibt zwei Versionen des Zumo 32U4 mit verschiedenen Gyroskop-ICs) können in der Empfindlichkeit und dem Messbereich eingestellt werden. Hierbei gibt der Messbereich die maximal messbare Drehrate in Grad pro Sekunde an und die Empfindlichkeit gibt die Genauigkeit der Messung an. Je kleiner der Wert der Empfindlichkeit, desto genauer der ermittelte Messwert.

In der Konfiguration für das Messen von Roboterdrehungen

imu.configureForTurnSensing();        // Empfindlichkeit und Filter einstellen

beträgt die Empfindlichkeit des Gyroskops 70 mdps/digit (Milligrad pro Sekunde / digit). Mit der eingestellten Empfindlichkeit ist es dann möglich, die Winkelgeschwindigkeit in Grad pro Sekunde zu bestimmen:

// Bestimmung der Winkelgeschwindigkeit (Drehrate) aus den Messwerten
// und der eingestellten Empfindlichkeit von 70 mdps/digit = 0.07 dps/digit
float winkelGeschw = imu.g.z * 0.07;   // in deg/s (Gradmaß pro Sekunde) mit Offset-Fehler

Wird der Offset-Fehler berücksichtigt, ergibt sch folgende Winkelgeschwindigkeit:

float winkelGeschw = (imu.g.z - offSet) * 0.07; // ohne Offset-Fehler in deg/s

Integration der Drehgeschwindigkeit​

Von der Theorie her ist bekannt, dass sich der aktuelle Drehwinkel aus der Integration der Drehgeschwindigkeit über die Zeit ergibt. Der Arduino kann die Integration dann als Aufsummierung der Winkelgeschwindigkeit unter Berücksichtigung der Zeitintervalle dt bestimmen.

winkel = winkel + winkelGeschw * dt

Das Zeitintervall dt entspricht der vergangenen Zeit seit der letzten Aktuallisierung des aktuellen Drehwinkels winkel und sollte möglichst klein sein. Daher sollte für dessen Bestimmung die micros() Funktion verwendet werden, welche die seit dem Programmstart vergangene Zeit in Mikrosekunden (µs) angibt und daher deutlich genauer ist als die millis() Funktion ist.

long now = micros();                  // Zeit in Mikrosekunden (µs)
long dt  = now - gyroLastUpdate;      // Zeitdifferenz in Mikrosekunden (µs) 
gyroLastUpdate = now;                 // `gyroLastUpdate` sollte global deklariert sein

In der folgenden Abbildung ist exemplarisch der gemessene Verlauf der kalibrierten Winkelgeschwindigkeit und des sich daraus ergebenen aktuellen Drehwinkels dargestellt.

Messfehler​

Wird über einen längeren Zeit der aktuelle Drehwinkel eines ruhenden Roboters bestimmt, ist man schnell verwundert, dass - obwohl in Ruhe - sich der ermittelte Drehwinkel des Roboters ändert. Je länger gewartet wird, desto schneller scheint sich der aktuelle Drehwinkel zu ändern. Die Ursache sind Messfehler, welchen bei jedem Gyroskop auftreten und verschiedene Ursachen haben. Die beiden wichtigsten Fehlerquellen sollen im Folgenden besprochen werden.

Veränderlichkeit des Offset-Fehlers (Bias Instability)​

Jedes Gyroskop erfährt den sogenannten Offset-Fehler, wodurch auch bei einem ruhenden Sensor Messwerte ungleich null gemessen werden. (Die Messwerte täuschen also eine Drehung bei einem ruhenden System vor.) Wie bereits weiter oben beschrieben, kann dieser Offset-Fehler durch einfaches Bestimmen des mittleren Offsets korrigiert werden. Problemtisch ist jedoch, dass der Offset- Fehler zeitlich nicht konstant ist. Äußere Effekte wie Temperaturänderungen oder Erschütterungen verändern den Offsetfehler und führen damit über eine längere Zeit zu fehlerhaften Messwerten. Eine regelmäßige Neukalibrierung des Sensors kann hier Abhilfe schaffen.

Random Walk​

Eine weitere Fehlerquelle bei der Bestimmung des aktuellen Drehwinkels ist der sogenannte Random Walk oder auch Irrfahrt. Es beschreibt die Verkettung mehrerer fehlerbehafteter Messgrößen, wobei diese einem zeitdiskreten stochastischem Prozess mit unabhängigen und identisch verteilten Änderungen unterliegen.

Werden beispielsweise gleichverteilte Zufallszahlen zwischen -5 und 5 aufaddiert, so ergibt sich zum Beispiel die folgende Zahlenfolge:

Zufallszahlen:        -1  +5   -1   -2   +2   +2   +5   +3   -4   -3   -5   +3  -3
Aufaddierte Werte:    -1   4    3    1    3    5   10   13    9    6    1    4   1

Hierbei erscheint es nicht ganz unplausibel zu vermuten, dass der Erwartungswert der aufaddierten Zahlen bei jedem Schritt 0 ist. Tatsächlich ist der Erwartungswert beim Random Walk immer 0, jedoch wächst mit jedem Schritt auch die Abweichung der Werte vom Erwartungswert (die Standardabweichung wächst).

In dem unten abgebildeten Radom Walk Simulator ist gut zu erkennen, dass jeder neue Random Walk (Hinzufügen neuer Werte durch Mausklick) einen anderen Weg geht und letztlich auch andere, meistens vom Erwartungswert 0 abweichende Werte, aufweist. Werden ganz viele Werte hinzugefügt (Starten der Animation mit 'a'), lässt sich die Verteilung des absoluten Häufigkeiten als Balkendiagramm darstellen. An dieser Verteilung wird ganz gut ersichtlich, dass je länger der Pfad eines Random Walks ist (also je mehr Messwerte aufaddiert werden), desto größer wird auch die Standardabweichung der aufsummierten Werte.

Für die Ermittlung des aktuellen Drehwinkels mit einem Gyroskop bedeutet dies, dass auch im Fall eines ruhenden Sensors mit der Zeit aus der Summe der Drehraten Drehwinkel berechnet werden, die vom Erwartungswert 0 abweichen. Es wird also immer wahrscheinlicher, dass bei langen Messreihen der ermittelte Drehwinkel von dem eigentlichen Drehwinkel abweichen wird.

Random Walk spielt außer beim Gyroskop auch in vielen andern Kontexten, wie zum Beispiel der Finanzmarktanalyse oder der Analyse von zufälligen Bewegungen von Teilchen in der Physik, ein große Rolle.

Aufgaben

  1. Welche Annahmen bzw. Näherungen werden gemacht, damit der Arduino aus der momentanen Winkelgeschwindigkeit des Gyroskops den Drehwinkel bestimmen kann?

  2. Analysieren Sie den Verlauf der Winkelschwindigkeit und des resultierenden aktuellen Drehwinkels in obiger Abbildung. Beschreiben Sie detailliert, welche Drehbewegungen der Roboter erfährt und in welcher Ausrichtung er sich jeweils befindet.

  3. Schreiben Sie ein Programm, welches das Gyroskop auf Tastendruck automatisch kalibriert und kontinuierlich den aktuellen Drehwinkel des Roboters auf dem Display ausgibt. Implementieren Sie hierfür die Funktion kalibrierenGyro() zum bestimmen des Offset-Fehlers und die Funktion updateWinkel(), welche bei jedem Aufruf den Drehwinkel aktualisiert.

    Während der aktuelle Winkel nur ca. all 200 ms auf dem Display ausgegeben werden sollte, muss updateWinkel() sooft wie möglich aufgerufen werden.

  4. Lassen Sie den Roboter mit Hilfe des Gyroskops auf der Stelle drehen. Implementieren Sie hierfür eine Funktion drehenGyro(int pGrad), welche den Roboter um die angegebene Gradzahl (auch negative Winkel) drehen lässt.

    Testen Sie die Funktion, indem Sie den Roboter um +180 Grad und anschließend -180 Grad drehen lassen.

  5. Lassen Sie den Roboter ein möglichst exaktes Quadrat mit einer Kantenlänge von 20 cm fahren. Nutzen Sie sowohl die Motorencoder als auch das Gyroskop.