Lokalisierung und Odometrie eines Roboters mit differentiellem Antrieb

Odometrie ist das Vorgehen, wie aus den Daten eines Vortriebsystems (Räder, Propeller, etc.) die Position und die Lage eines Objektes im Raum bestimmt wird. Im Fall eines Roboters mit differentiellem Antrieb also, wie mit Hilfe der möglichst exakten Messung der Radumdrehungen die Position des Roboters in der Ebene (x,y) und dessen Orientierung $\vartheta$ bestimmt wird.

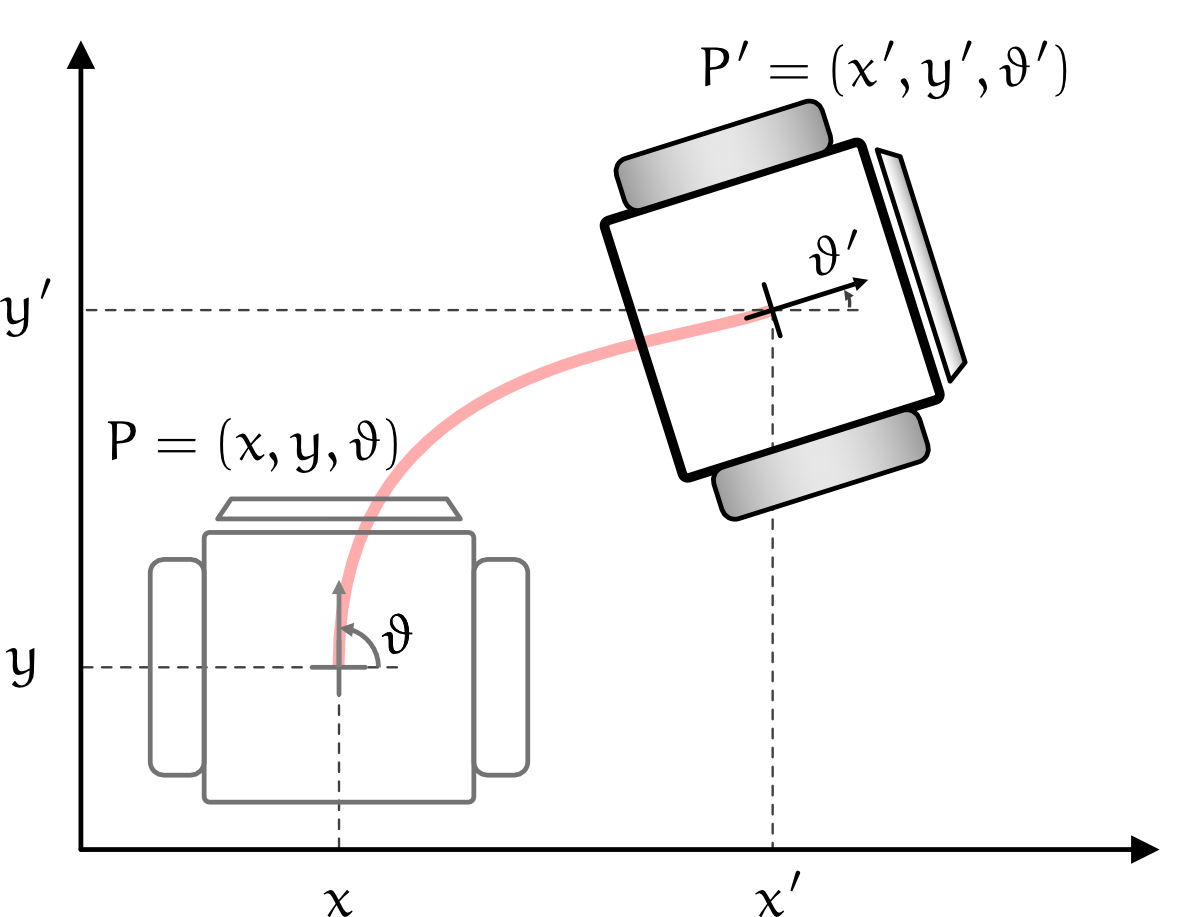
Mit der Odometrie kann die Position und die Orientierung eines Roboters nur relativ zur letzten bekannten Lage ermittelt werden. Ist die Ursprungslage $P=(x,y,\vartheta)$ des Roboters bekannt, lässt sich mit den Radumdrehungen die Positionsänderung ($\Delta x, \Delta y, \Delta \vartheta$) und somit die neue Position $P'=(x',y',\vartheta')$ bestimmen.

ACHTUNG

Die Orientierung $\vartheta$ des Roboters bezieht sich auf die x-Achse. Ist der Roboter z.B. nach Norden ausgerichtet, beträgt die Orientierung $\vartheta = 90°$ $(\vartheta = \frac{\pi}{2})$.

Den Roboter auf der Stelle drehen lassen

Wenn der Roboter geradeaus fährt, kann die zurückgelegte Strecke relativ einfache durch die Anzahl der Encoder-Impulse mal der Encoder-Auflösung berechnet werden. Allerdings reicht die zurückgelegte Entfernung alleine zur Postionsbestimmung nicht aus. Zusätzlich ist auch immer die Orientierung, also die Richtung, in welche der Roboter zeigt, wichtig.

Der einfachste Fall zur Bestimmung der Orientierung ist die Drehung des Roboters auf der Stelle. In diesem Fall drehen sich beide Räder gleich schnell, jedoch in verschiedene Richtungen. Idealerweise sollten sich die Koordinaten (x,y) des Roboters dabei nicht ändern.

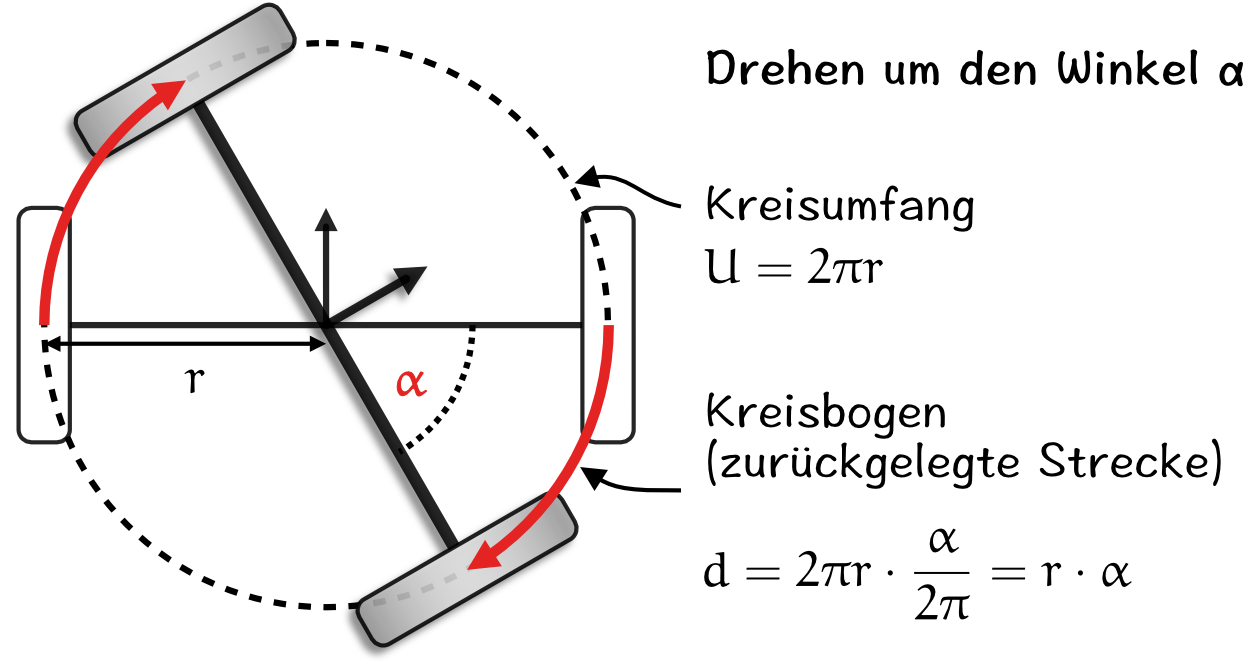
Zur Berechnung des Drehwinkels $\alpha$, also der Änderung der Orientierung $\Delta \vartheta$ genügt es, die zurückgelegte Strecke der beiden Räder auf dem Kreis (Länge des Kreisbogens) zu bestimmen.

Mit den Umfang eines Kreises $U$ lässt sich über eine Verhältnisgleichung die Länge eines Kreisbogens $d$ berechnen. Hierbei gilt, dass das Verhältnis vom Kreisumfang $U$ zu dem Winkel $2\pi$ (entspricht 360°) gleich dem Verhältnis vom Kreisbogen $d$ zum Drehwinkel $\alpha$ ist:

$$\frac{U}{2\pi} = \frac{d}{\alpha}.$$

Da für den Kreisumfang $U = 2\pi r$ gilt, folgt die Gleichung:

$$\frac{2\pi \cdot r}{2\pi} = \frac{d}{\alpha}.$$

Gekürzt und nach der Länge des Kreisbogens umgestellt, ergibt sich:

$$r \cdot \alpha = d.$$

Der Drehwinkel $\alpha$ ergibt sich also aus der Länge des Kreisbogen $d$ geteilt durch den Radius $r$ :

$$\alpha = \frac{d}{r}.$$

Der Radius $r$ entspricht dem halben Radabstand und der Kreisbogen $d$ kann mittels der Motor-Encoder bestimmt werden.

caution

Bei der Gleichung für den Drehwinkel müssen die Winkel im Bogenmaß $(0 \cdots 2\pi)$ angegeben werden.

Programmieren einer Funktion zum Drehen auf der Stelle

Die obige Funktion für den Drehwinkel $\alpha$ kann gut verwendet werden, um den Roboter auf der Stelle um einen angegebenen Winkel drehen zu lassen. Hierfür muss zuerst zuerst der halbe Radabstand $r$ des Roboters bestimmt werden. Anschließend müssen folgende Berechnung vorgenommen werden:

1. Bestimmen des zurückgelegten Weges $d$ der Räder mit Hilfe der Encoder-Impulse und der Encoder-Auflösung (ca. 0,128 mm/Impuls).
2. Umrechnen des Drehwinkels vom Bogenmaß (Radiant) in Grad.

// Konstanten zum Umrechnen von Grad in Bogenmaß sollten per #define angegeben werden
#define PI 3.14159265359
#define RADtoDEG 57.2957795131 // = 180/pi
#define DEGtoRAD 0.01745329252 // = pi/180
#define MMperTICK  0.282       // Auflösung der Radencoder (3pi+ Standard)

// Funktion zum Drehen des Roboters 
void drehen(float pWinkelDEG){
  /* -----------------------------------
   1. Umrechnen des Winkels in Bogenmaß (RAD).
   2. Anzahl der notwendigen Motor-Impulse für den gegebenen Drehwinkel 'pWinkelRad' bestimmen.
   4. Drehe den Roboter solange, bis die notwendigen Motor-Impulse erreicht wurden
   5. Stoppe den Roboter. 
   ------------------------------------- */
}

Da Berechnungen mit Fließkommazahlen (float) auf dem Arduino relativ langsam sind, ist es ratsam die Umrechnung des Winkelmaßes nicht ständig, sondern nur einmal an geeigneter Stelle vorzunehmen.

Aufgaben

1. Bei einem Roboter, der sich auf der Stelle dreht, wurden durch die Rad-Encoder jeweils 400 Impulse in unterschiedliche Richtungen gezählt. Der Radabstand des Roboters beträgt 10 cm und die Auflösung des Encoders beträgt 0,1 mm pro Impuls. Bestimmen Sie den Drehwinkel $\alpha$ des Roboters.

2. Schreiben Sie eine Funktion void drehenWinkel(int pWinkel), welche den Roboter mit den Encodern um den angegebenen Winkel drehen lässt. Ein negativer Winkel dreht den Roboter im Uhrzeigersinn. Testen Sie die Funktion, indem Sie den Roboter nacheinander um folgende Winkel drehen lassen:

   1. +45°, - 45°
   2. +90°, -90°
   3. +180°, -180°
   4. +360°, - 360°

   Analysieren Sie anschließend die Genauigkeit der Drehungen.

3. Schreiben Sie eine Funktion void fahren(int pDistanzMM), welche den Roboter eine gerade Strecke mit der angegebenen Distanz fahren lässt. Nutzen Sie beiden Funktionen, um folgende Strecken zu fahren:

   1. Ein Rechteck mit einer Kantenlänge von 30 cm.
   2. Ein gleichschenkliges, rechteckiges Dreieck, dessen Hypothenuse (Basis) 20 cm lang ist. Hinweis: Berechnen Sie zuerst die Länge der Katheten und die unbekannten Winkel.
   3. Das Haus vom Nikolaus.

Vollständige Kinematik

Bisher ist der Roboter entweder gerade gefahren oder hat sich auf der Stelle gedreht. Das heißt, entweder haben sich die Koordinaten $(x,y)$ oder die Orientierung $\vartheta$ hat sich geändert. Beides zur selben Zeit hat sich bisher noch nicht geändert.

Im folgenden soll daher untersucht werden, wie sich die Position eines Roboters $P=(x,y,\vartheta)$ ändert, wenn durch die Drehung der Räder nicht nur einer Änderung der Koordinaten $(\Delta x, \Delta y)$, sondern auch eine Änderung der Orientierung $\Delta \vartheta$ auftritt.

In der Abbildung ist ein Roboter dargestellt, der einen Kreisbogen entlangfährt. Mit Hilfe der Rad-Encoder kann der zurückgelegte Weg des linken $d_\text{L}$ und des rechten Rades $d_\text{R}$ bestimmt werden. Gesucht ist nun die sich ergebende Position $P'$ des Roboters, also die neuen Koordinaten $(x',y')$ und die Orientierung $\vartheta'$.

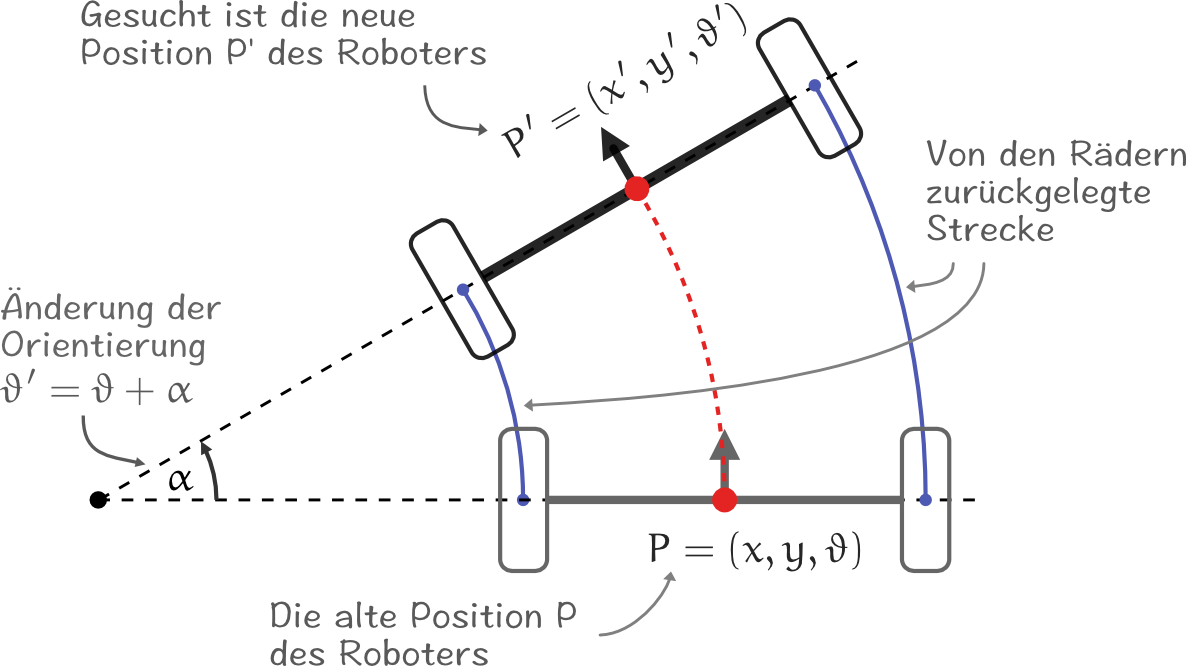
Berechnung des Drehwinkels $\alpha$

Die neue Orientierung $\vartheta'$ lässt sich sehr einfach aus der alten Orientierung $\vartheta$ und dem Drehwinkel $\alpha$ bestimmen:

$$\vartheta' = \vartheta + \alpha$$

Aber wie kann der Drehwinkel $\alpha$ bestimmt werden? Wie oben gezeigt wurde, gilt für die Länge eines Kreisbogens $d = \alpha\cdot r$.

Anders, als es im letzten Abschnitt angenommen wurde, kann mit den Rad-Encodern die Länge des Kreisbogens nicht exakt bestimmt werden. Mit einem Rad-Encoder können Entfernung nur diskret, also als Vielfaches der Encoderauflösung (z.B. 0.1 mm pro Impuls) gemessen werden. Das bedeutet, dass die zwischen zwei Encoder-Impulsen bestimmte Strecke nicht die Länge des Kreisbogens ist, sondern die Strecke zwischen zwei Punkten (in der Abbildung blau gestrichelt dargestellt). Wenn der Drehwinkel jedoch sehr klein ist, kann die gemessene Strecke gut als Näherung für den Kreisbogen angesehen werden.

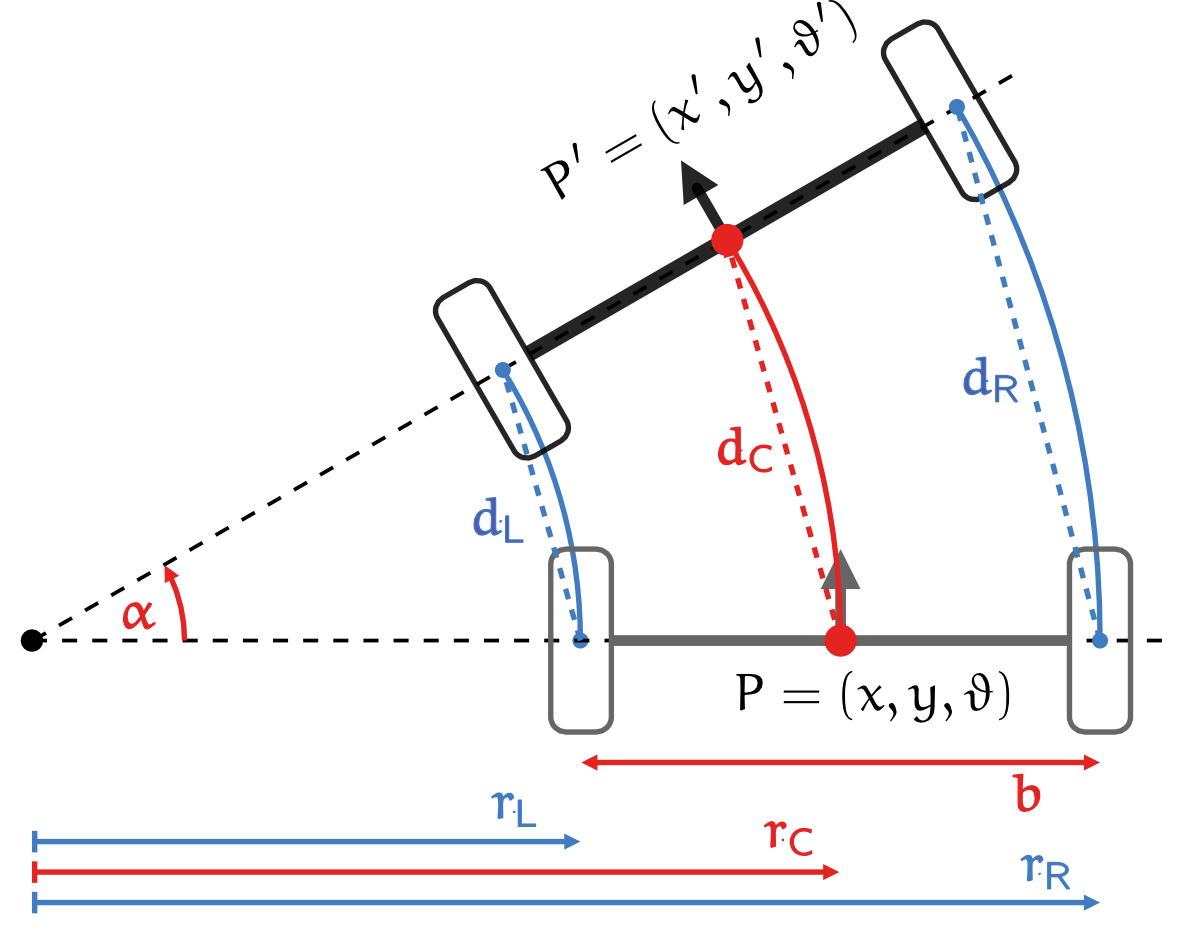
Der Drehwinkel $\alpha$ ergibt sich damit aus den Verhältnissen von zurückgelegter Strecke $(d_\text{L},d_\text{C},d_\text{R})$ und den zugehörigen Drehradien $(r_\text{L},r_\text{C},r_\text{L})$:

$$\begin{aligned} \alpha = \frac{d_\text{L}}{r_\text{L}}, \; \alpha = \frac{d_\text{C}}{r_\text{C}}, \; \alpha = \frac{d_\text{R}}{r_\text{R}} \end{aligned}$$

Mit den Gleichungen für das linke und rechte Rad lässt sich der Drehwinkel $\alpha$ bestimmen:

$$\begin{aligned} \alpha \cdot r_\text{R} &= d_\text{R} \\ \alpha \cdot r_\text{L} &= d_\text{L} \end{aligned}$$

Wird die Differenz der beiden Gleichungen gebildet, folgt:

$$\begin{aligned} \alpha \cdot ( r_\text{R} - r_\text{L})= d_\text{R}- d_\text{L} \end{aligned}$$

Da die Differenz zwischen den Drehradien der beiden Räder genau dem Radabstand $b = r_\text{R} - r_\text{L}$ entspricht (siehe Abbildung), folgt für den Drehwinkel:

$$\alpha = \dfrac{d_\text{R}- d_\text{L}}{r_\text{R} - r_\text{L}}= \dfrac{d_\text{R}- d_\text{L}}{b}$$

Vergleich mit Auf der Stelle drehen

Vergleicht man die Gleichung für den Drehwinkel $\alpha$ mit der Gleichung aus dem Abschnitt Den Roboter auf der Stelle drehen lassen, so sollte die zuletzt hergeleitete Gleichung bei einer Drehung auf der Stelle zum selben Ergebnis führen.

Dreht sich der Roboter auf der Stelle, sind die zurückgelegten Wege des linken und des rechten Rades bis auf das Vorzeichen gleich:

$$d_\text{R} = - d_\text{L}.$$

In obige Gleichung eingesetzt, ergibt sich damit:

$$\begin{aligned} \alpha = \frac{d_\text{R} + d_\text{R}}{ r_\text{R} - r_\text{L}} = \frac{2\cdot d_\text{R}}{ b} = \frac{2 \cdot d_\text{R}}{2\cdot r} = \frac{d_\text{R}}{r}. \end{aligned}$$

Das entspricht genau der Gleichung für den Drehwinkel eines sich auf der Stelle drehenden Roboters.

Berechnung der Koordinaten $(x',y')$

Die Koordinaten $(x,y)$ des Roboters beziehen sich auf den Mittelpunkt, also die Drehachse des Roboters. Daher ist es im ersten Schritt notwendig, die Länge des Kreisbogens $d_\text{C}$, den der Mittelpunkt des Roboters zurücklegt, zu bestimmen. Da der Drehradius $r_\text{C}$ des Robotermittelpunktes genau der Mittelwert der Drehradien der beiden Räder ist $r_\text{C} = (r_\text{R}+r_\text{L})/2$, folgt:

$$\begin{aligned} d_\text{C} &= \alpha \cdot r_\text{C}\\ d_\text{C} &= \alpha \cdot \frac{r_\text{R}+r_\text{L}}{2} \end{aligned}$$

An dieser Stelle können die Drehradien der einzelnen Räder ersetzt werden mit $r_\text{R} = d_\text{R}/\alpha$ und $r_\text{L} = d_\text{L}/\alpha$. Somit ergibt sich für den zurückgelegten Weg des Robotermittelpunktes $d_\text{C}$:

$$\begin{aligned} d_\text{C} &= \frac{\alpha}{2} \cdot \left(\frac{d_\text{R}}{\alpha}+\frac{d_\text{L}}{\alpha}\right)\\ d_\text{C} &= \frac{d_\text{R}+d_\text{L}}{2}. \\ \end{aligned}$$

Im nächsten Schritt werden aus dem berechneten Weg $d_\text{C}$ mithilfe des Drehwinkels $\alpha$ die Änderungen der Koordinaten $(\Delta x, \Delta y)$ berechnet werden. Damit können anschließend die neuen Koordinaten des Roboters bestimmt werden:

$$(x',y') = (x+ \Delta x , y+\Delta y)$$

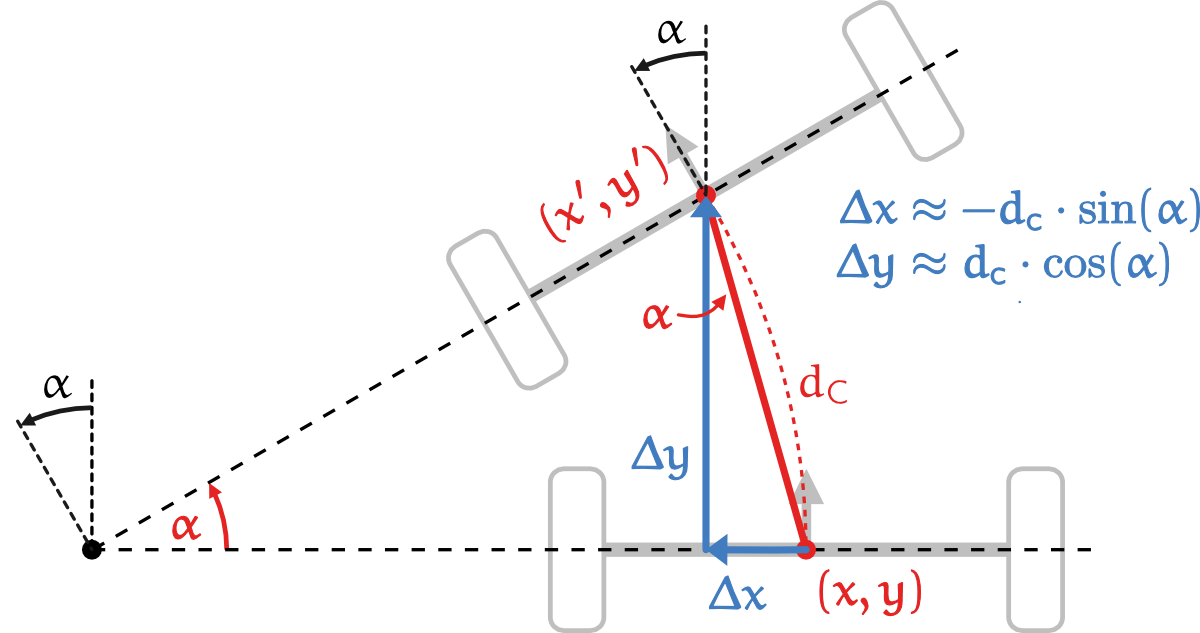
Zur Bestimmung von $(\Delta x, \Delta y)$ kann ein rechtwinkliges Dreieck zwischen den Koordinaten $(x,y)$ und $(x',y')$ aufgespannt werden. Wenn der zurückgelegte Weg des Roboters (bzw. der Drehwinkel $\alpha$) klein ist, können für das Dreieck folgende Näherungen gemacht werden:

• Die Länge des Kreisbogens, den der Roboter zurückgelegt hat, entspricht der Entfernung zwischen den Koordinaten $(x,y)$ und $(x',y')$
• Die Hypotenuse des abgebildeten rechtwinkligen Dreiecks entspricht $d_\text{C}$.
• Der obere Winkel des rechtwinkligen Dreiecks entspricht dem Drehwinkel $\alpha$.

Damit ergeben sich für die Länge der Katheten $\Delta x$ und $\Delta y$ folgende Gleichungen:

$$\begin{aligned} \Delta x &\approx - d_\text{c}\cdot \sin(\alpha)\\ \Delta y &\approx \;\; d_\text{c}\cdot \cos(\alpha) \end{aligned}$$

Das negative Vorzeichen bei $\Delta x$ ergibt sich dadurch, das die Änderung der x-Koordinate negativ ist.

Bewegungsgleichungen

Die oben hergeleiteten Gleichungen beziehen sich alle auf den Drehwinkel $\alpha$. Praktischer ist es jedoch, die sich ändernden Koordinaten $(\Delta x, \Delta y)$ auf die aktuelle, bzw. die sich ergebende Orientierung $\vartheta$ bzw. $\vartheta'$ des Roboters zu beziehen. Der Zusammenhang zwischen beiden Winkeln ist in der Abbildung dargestellt.

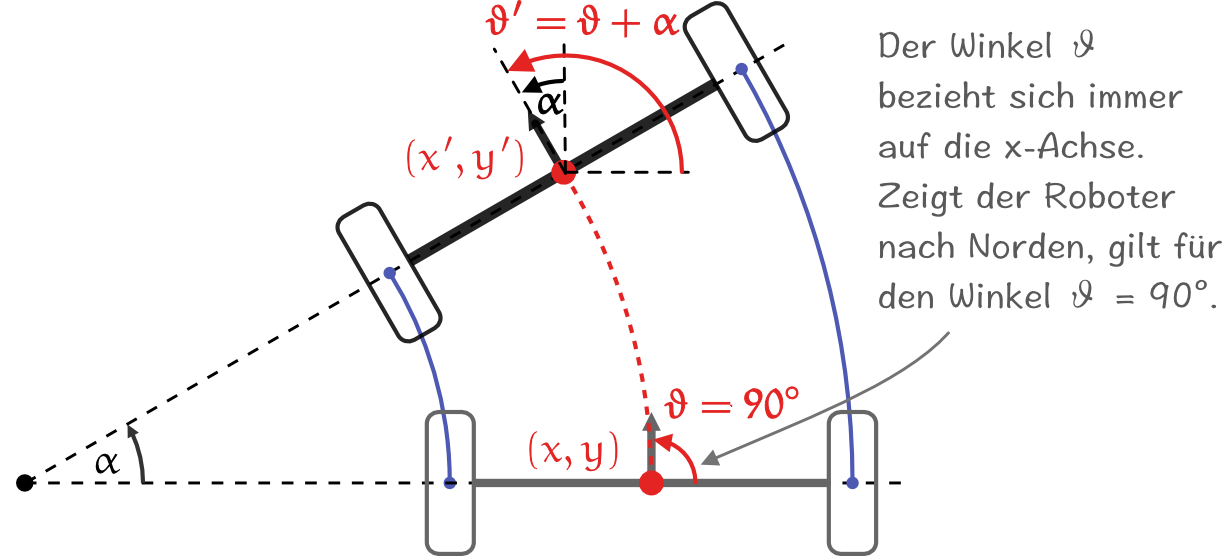
Die Orientierung $\vartheta$ bezieht sich immer auf auf den Mittelpunkt des Roboters und die x-Achse, während sich der Drehwinkel (wenn er am Mittelpunkt des Roboters angelegt ist) auf die y-Achse bezieht. Dieser Unterschied von 90$^\circ$ führt zu einer Änderung der Bewegungsgleichungen wenn sie auf die Orientierung $\vartheta$ anstatt auf den Drehwinkel $\alpha$ bezogen werden.

$$\begin{aligned} \Delta x &= d_\text{c}\cdot \cos(\vartheta)\\ \Delta y &= d_\text{c}\cdot \sin(\vartheta)\\ \alpha &= \frac{d_\text{R}- d_\text{L}}{b} \end{aligned}$$

Wobei $d_\text{C}$ die mittlere Weglänge der Räder darstellt:

$$d_\text{C} = \frac{d_\text{R}+d_\text{L}}{2}$$

Die neue Postion des Roboters lässt sich dann als die alte Postion plus der Positionsänderung beschreiben:

$$\begin{aligned} x' &= x + \Delta x\\ y' &= y + \Delta y\\ \vartheta' &= \vartheta +\alpha \end{aligned}$$

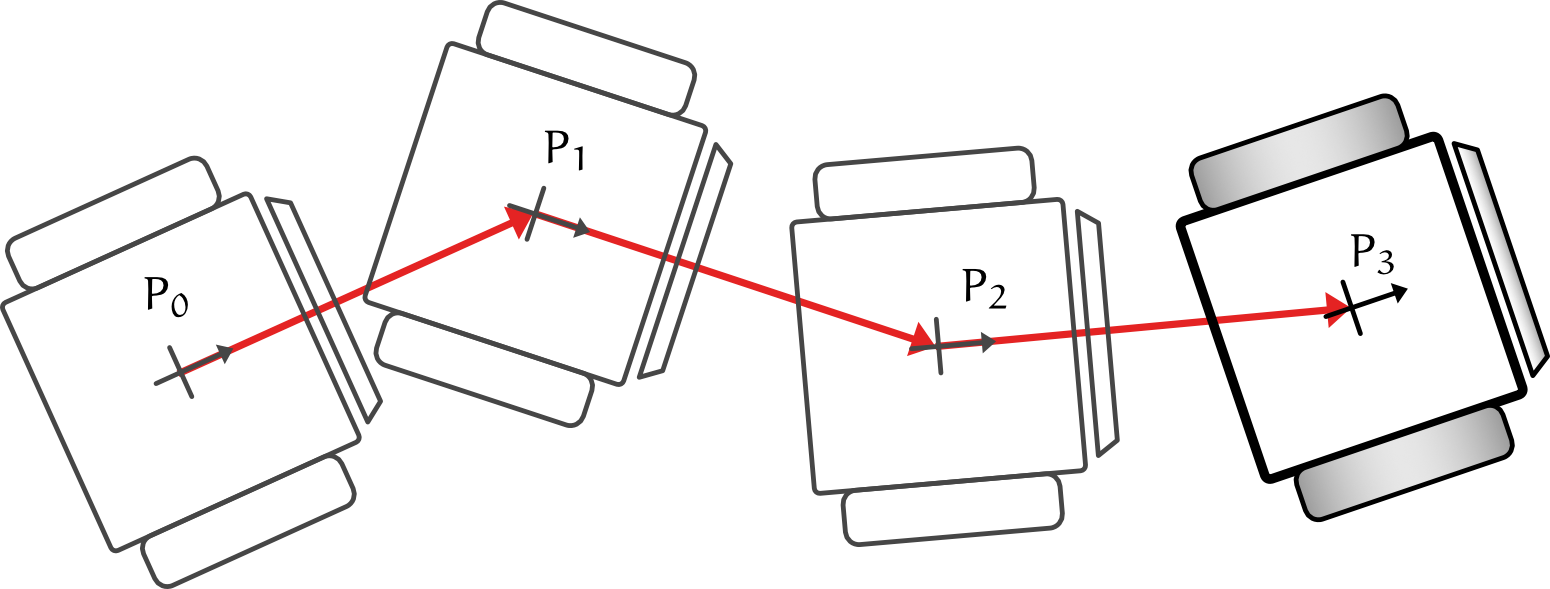
Wird die Berechnung der neuen Koordinaten wiederkehrend durchgeführt, so kann der vom Roboter zurückgelegte Weg als Verkettung von geraden Wegstücken (siehe Abbildung unten) abgeschätzt werden.

Aufgaben

1. Die aktuelle Position des Roboters ist x = 50 mm, y = 40 mm und ϑ = 60°. Mit dem Encoder wurden für das linke Rad +32 und das rechte Rad +53 Impulse gemessen. Bestimmen Sie die neue Position (x',y',ϑ'). (Radabstand 85 mm, Encoderauflösung 0.282 mm/Tick).

2. Ein Roboter (Radabstand 85 mm, Encoderauflösung 0.282 mm/Tick) mit der Startposition x = 0 mm, y = 0 mm, ϑ = 0 fährt eine bestimmte Wegstrecke zweimal ab. Bei jeder Fahrt werden unterschiedlich viele Messungen mit den Motorencodern vorgenommen. Die folgende Anzahl an Encoder-Impulsen wurde in den beiden Fällen ermittelt:

   1. Bei vier Messungen jeweils

      links  = -36.7
      rechts = 436.7

   2. Bei acht Messungen jeweils

      links  = -18.4
      rechts = 218.4

   Berechnen Sie die einzelnen Wegpunkte des Roboters und zeichnen sie für beide Fälle den sich ergebenen Fahrtweg in ein geeignetes Koordinatensystem. Vergleichen Sie für beide Fälle die insgesamt zurückgelegte Wegstrecke (Summe der Teilwegstrecken $d_c$) und überlegen Sie, welchen Weg der Roboter tatsächlich abgefahren sein könnte.

3. Schreiben Sie ein Programm, welches die aktuelle Position (x, y, ϑ) fortlaufend ermittelt und auf dem Display ausgibt. Testen Sie die Positionsbestimmung indem der Roboter einer Linie folgt.

4. Ein Roboter folgt vom Startpunkt (x=0, y=0, ϑ=0°) verschiedenen Linien bis zum Ende. Berechnen Sie für die erreichten Positionen die Länge des direkten Weges zurück zum Startpunkt und den Drehwinkel, damit sich der Roboter zum Ursprung ausrichten kann. Skizzieren Sie für jede Rechnung auch die Lage des Roboters im Koordinatensystem.

   1. x = 150 mm, y = 300 mm, ϑ= -90°
   2. x = 150 mm, y = 300 mm, ϑ= 130°
   3. x = 200 mm, y = -150mm, ϑ= 0°
   4. x = 200 mm, y = -150mm, ϑ= -130°

5. Erweitern Sie das Programm zur Positionsbestimmung aus Aufgabe 3. Nun soll der Roboter einer Linie folgen und am Ende auf direktem Weg in einer gerade Linie zu seinem Startpunkt zurückkehren (ohne der Linie zu folgen).

6. Lassen Sie den Roboter einem auf Papier gezeichnetem Oval mehrmals nacheinander folgen. Bestimmen Sie währenddessen die aktuelle Position und speicher Sie diese in einem Array. Übetragen Sie die Positionsdaten im Anschluss auf den PC und stellen sie diese geeignet graphisch dar (z.B. mit einem einfachen Liniendiagramm in Excel oder OpenOffice). Analysieren Sie die ermittelte Wegstrecke. Entspricht sie dem wirklich abgefahrenem Weg?

   Versuchen Sie die Genauigkeit der Positionsbestimmung durch das Kalibrieren der Motoren zu verbessern.

Links

• Control of Mobile Robots- 2.2 Differential Drive Robots (Youtube)
• Elements of Robotics: Robotic Motion and Odometry (Springer)