Linienfolger mit einem Proportional-Regler

Der einfache 3-Stufen Algorithmus zum Folgen einer Kante (oder Linie) funktioniert bei Linien und Abzweigung meistens ganz gut, lässt aber den Roboter die Linie entlangzappeln, anstatt ihr geschmeidig zu folgen. Auch wird es mit dem einfachen Algorithmus schwierig, dem Roboter bei Kreuzungen oder Abzweigung ein konkretes Verhalten zu programmieren.

Ein wesentlich besserer Ansatz ist der Proportional-Regler (P-Regler), bei dem es nicht nur drei verschiedene Unterscheidungsstufen mit drei verschiedenen Motordrehzahlen gibt, sondern für jeden Unterschied zwischen Soll- und Istwert ein geeigneter Wert zum Steuern der Motoren berechnet wird.

Regelkreis (control system)

Bevor jedoch der P-Regler für den Linienfolger entwickelt wird, soll kurz die allgemeine Struktur eines Regelkreises (control system) anhand des Linienfolger erläutert werden.

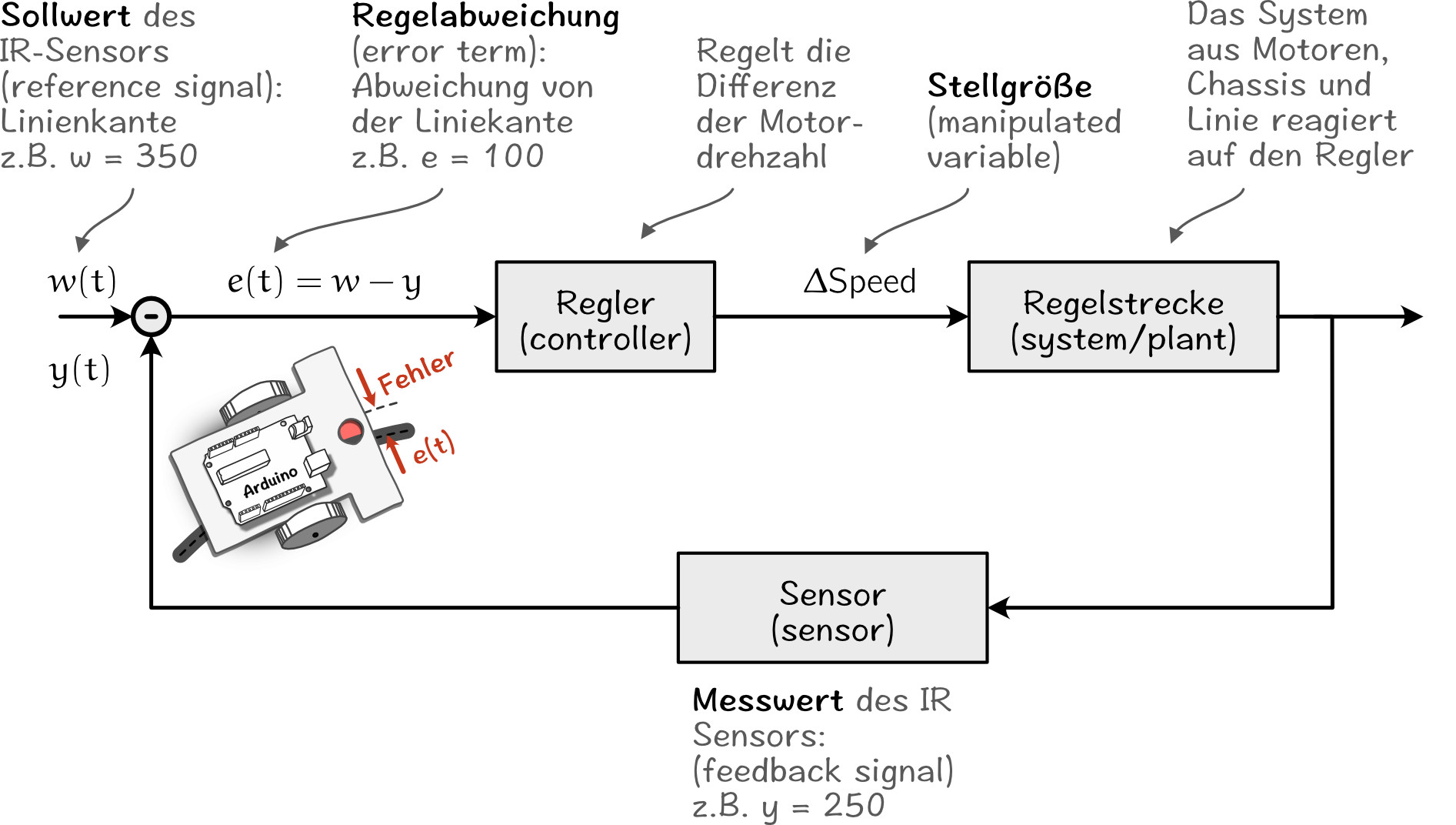
Bei einem Regelkreis (control system) wird davon ausgegangen, dass ein System einen Sollwert $w(t)$ (engl. reference signal) einhalten soll. In unseren Fall ist die Sollgröße der vom Sensor zu erzielende Sensorwert der Linienkante (z.B. 350).

Weicht der Messwert $y(t)$ , also der aktuell gemessene Sensorwert von der Sollgröße ab, so lässt sich die Regelabweichung (auch error term oder Fehlerwert) $e(t)$ leicht als Differenz aus Soll- und Messwert berechnen: $e(t) = w(t) - y(t)$ .

Mit Hilfe der Regelabweichung $e(t)$ bestimmt nun der Regler (engl. controller) die Stellgröße (engl. manipulated variable), welche auf die Regelstrecke (engl. system oder plant) einwirkt. In diesem Fall ist die Regelstrecke der Roboter, welcher der Kante folgen soll. Ein anderes Beispiele ist ein Tempomat, bei dem die Geschwindigkeit eines Fahrzeugs konstant gehalten werden soll.

In der Regel ist das Ziel eines Reglers, den zeitveränderlichen Fehlerwert so klein wie möglich zu halten und damit den Messwert an den Sollwert anzunähern. Im Fall des Kantenfolgers bedeutet dies, dass der Roboter möglichst immer über der Kante bleibt.

Aufgaben Regelkreis

Aufgaben

Skizzieren Sie den Regelkreis für einen PKW-Tempomat und erläutern Sie die zugehörigen Größen des Regelkreises (Sollwert, Messwert, Regelabweichung, Stellgröße, Regelstrecke).
Geben Sie 5 technische Beispiele für einen Regelkreis an.
Diskutieren Sie, welche sinnvoll zu regelnden Größen es bei einem Roboter geben könnte.

Proportional-Regler (P-Controller)

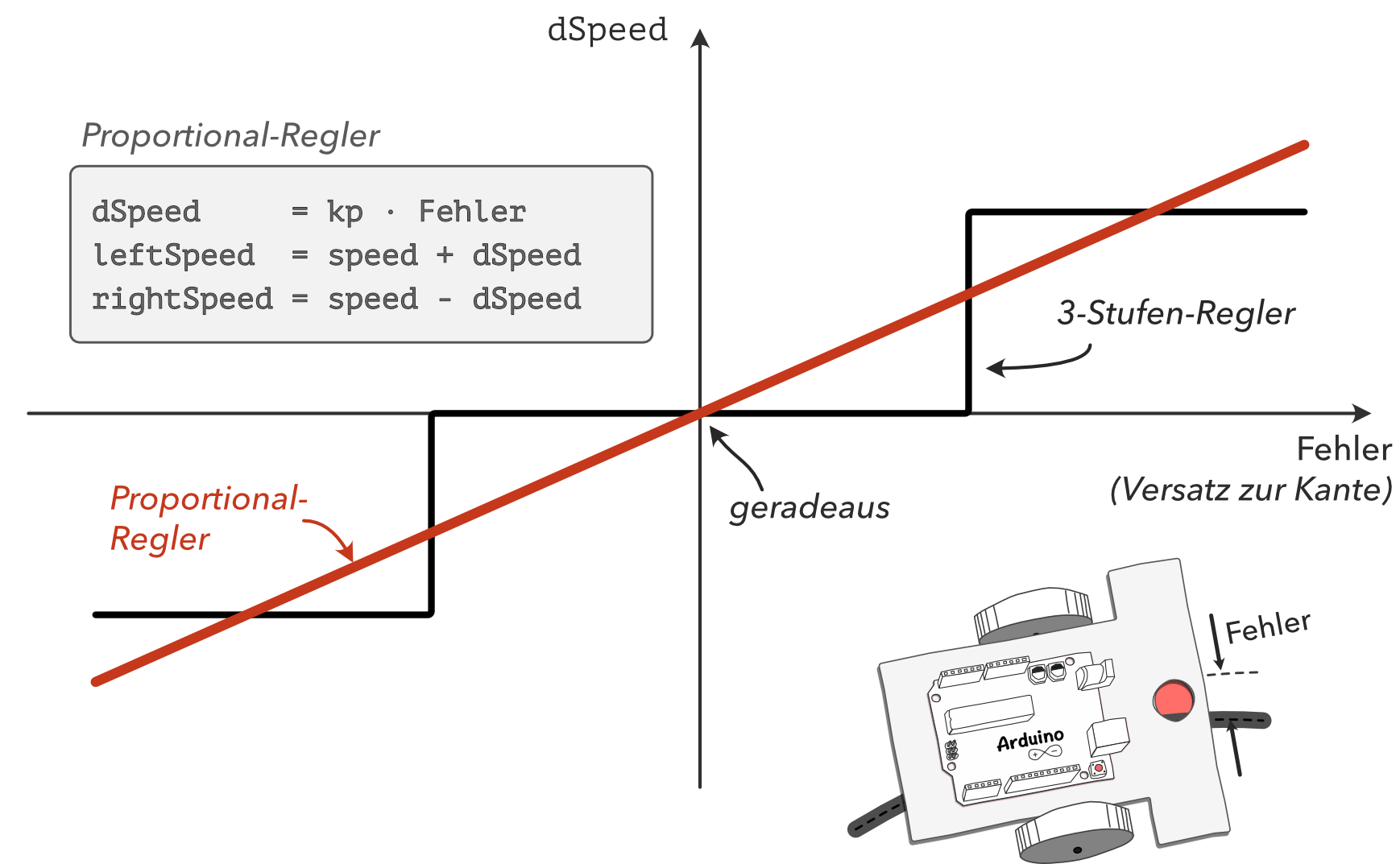
Im Gegensatz zu einem 3-Stufen-Regler, bei dem nur drei verschiedene Motordrehzahlen für das Kurvenverhalten eingestellt werden, gibt es bei dem P-Regler einen proportionalen Zusammenhang zwischen der Regelabweichung $e(t)$ und der Stellgröße (Motordrehzahl).

Konkret wird beim P-Regler die Abweichung der Motordrehzahl (dSpeed) von einer Normgröße (speed) gesteuert. Die aktuelle Motordrehzahl ergibt sich dann als Summe aus der Normgröße und der Abweichung. Damit der Roboter seine Fahrtrichtung ändern kann, wird dSpeed je nach Seite von der Normgröße (speed) abgezogen oder hinzuaddiert:

leftSpeed  = speed + dSpeed  // Drehzahl linkes Rad
rightSpeed = speed - dSpeed  // Drehzahl rechtes Rad

Die Abweichung der Motordrehzahl (dSpeed) hängt proportional von der Regelabweichung (Fehlerwert), also der Abweichung von der Linienkante ab. Mit dem Proportionalitätsfaktor $k_p$ wird dSpeed direkt aus der Regelabweichung berechnet:

dSpeed  = kp * e   // e: Regelabweichung, Fehlerwert

Die Regelabweichung $e(t)$ kann aus der Differenz des Sollwertes (also dem Wert der Linienkante) und dem Messwert des IR-Sensors bestimmt werden.

e = wertKante - sensorWert;     // Fehlerwert, Regelabweichung

Wahl des Faktors $k_p$

Die Wahl des Faktors $k_p$ hat einen erheblichen Einfluss auf das Fahrverhalten des Roboters.

Ist $k_p$ zu klein, wird der Fehler nicht schnell genug geändert und der Roboter wird bei einer Kurve ganz schnell die Kante verlieren. Der Fehler steigt also immer weiter an.
Ist $k_p$ jedoch zu groß gewählt, so fängt der Roboter an, hin- und herzuschwingen. In diesem Fall spricht man auch von einem oszillierenden Verhalten.
Diese Oszillationsbewegungen entstehen, weil auf relativ kleine Fehler mit einem zu starken Gegenlenken (also einem zu großen dSpeed) reagiert wird. Man kennt dieses Verhalten von Kindern, die Fahrrad fahren lernen. So lange, wie sie noch unsicher sind, wackeln sie stark mit dem Lenker, um das Gleichgewicht zu halten. Erst mit etwas mehr Übung wird ihr Fahrverhalten ruhiger und das Schlingern des Rades nimmt ab.
Ähnlich wie bei dem 3-Stufenregler hat die Geschwindigkeit des Roboters einen großen Einfluss auf das Ergebnis des Reglers. Beginnen Sie am besten mit einer geringen Geschwindigkeit. (Warum eigentlich?)

Begrenzung der ermittelten Geschwindigkeit: `constrain()`

In Abhängigkeit vom Proportionalitätsfaktor $k_p$ und der Regelabweichung (Fehlerwert) kann es passieren, dass die ermittelte Geschwindigkeit eines Rades den zulässigen Wertebereich von z.B. 0 bis 255 (PWM-Werte) überschreitet. In diesem Fall würde die Funktion analogWrite(pin,PWM) zur Geschwindigkeitssteuerung keinen Fehler ausgeben und trotzdem einen falschen PWM-Wert setzen. Daher sollten die berechneten PWM-Werte für die Motoren auf geeignete Werte begrenzt werden.

Hierfür eignet sich der Arduino-Befehl constrain(),

wertC = constrain(wert,min,max)

welche den Eingabewert wert auf den angegebenen Minimal- min und Maximalwert max begrenzt. Dabei gilt:

wertC = wert, wenn wert zwischen min und max
wertC = min, wenn wert kleiner min ist
wertC = max, wenn wert größer max ist

Pseudocode

Bevor ein Algorithmus (z.B. der P-Regler) in ein lauffähiges Programm überführt wird, ist es sinnvoll sich einen Pseudocode für den Algorithmus zu erstellen. Im Gegensatz zum echten Programmcode, kann der Pseudocode vom Arduino oder PC nicht gelesen bzw. korrekt interpretiert werden. Er dient vor allem zu Strukturierung und Veranschaulichung eines Algorithmus. Gibt es zu einem Algorithmus einen gut lesbaren Pseudocode, ist es meistens relativ einfach, diesen in die entsprechende Programmiersprache (z.B. Arduino) zu überführen.

Da der Pseudocode nicht von einer Maschine, sondern von Menschen gelesen werden soll, gibt es dafür auch kaum feste Regeln. Die wichtigste Regel ist jedoch, dass der Pseudocode selbsterklärend und verständlich sein soll. Einzelne Konzepte einer speziellen Programmiersprache (Objekte, Arrays, Pointer, etc.) sollten im Pseudocode nicht auftauchen. Auch kann auf Semikola am Zeilenende oder geschweifte Klammern für Programmblöcke verzichtet werden. Für eine gute Lesbarkeit sollten Programmblöcke für Verzweigungen und Schleifen im Code eingerückt werden.

An dem bereits bekannten Pseudocode für den 3-Stufen-Kantenfolger können einzelne Merkmal eines gut lesbaren Codes erläutert werden.

// Pseudocode eines 3-Stufen-Kantenfolgers
wertKante = 600                     // eine Variable

wiederhole dauerhaft                // Schleifen können mit `wiederhole` und
                                    // zugehörigen Bedingungen bezeichnet werden.
                                    // Der zugehörige Codeblock wird eingerückt.
    wertIr = messenIrSensor()       // Funktionen werden mit Klammern () markiert.
    wenn: wertIr > wertKante        // Programmverzweigungen mit `wenn`, 
                                    // `sonst wenn` und `sonst` bezeichnet werden.
        fahrenLinks() 
        
    sonst wenn: wertIr <= wertKante // Bedingungen können als Code oder auch
                                    // umgangssprachlich ausgedrückt werden.
        fahrenRechts() 

Aufgaben

Ein kalibrierter Roboter, welcher mit einer Geschwindigkeit von speed = 130 geradeaus fährt, ermittelt mit dem Bodensensor einen Messwert von sensorWert = 45. Der Sollwert des Reglers, also die Linienkante hat einen Wert von kante = 345.
1. Bestimmen Sie die Regeldifferenz $e$ .
2. Berechnen Sie den Wert für den Proportional-Faktor $k_p$ , damit sich eine Änderung der Motorgeschwindigkeit von dSpeed = 150 ergibt.
3. Ermitteln Sie die neuen Werte des linken und des rechten Motors (ohne Begrenzung des Wertebereichs).
4. Analysieren Sie die ermittelten PWM-Werte hinsichtlich des Fahrverhaltens des Roboters.
5. Wie ändert Sie das Fahrverhalten, wenn ein Proportional-Faktor $k_p = 1.2$ verwendet wird.
Wiederholen Sie die erste Aufgabe mit dem realen Wert der Linienkante Ihres Roboters. Schätzen Sie einen sinnvollen Werte für $k_p$ ab und begründen Sie Ihre Wahl.
Schreiben Sie den Pseudocode für einen Kantenfolger mit P-Regler.
Programmieren Sie einen Kantenfolger mit P-Regler. Welchen Einfluss hat die maximale Geschwindigkeit der Räder maxSpeed auf das Verhalten des Reglers? Welchen maximalen Wert können Sie für maxSpeed angeben, damit der Roboter die gesamte Strecke schafft? Optional: Nutzen Sie die Taster, um den Wert für kp direkt am Roboter zu ändern.

Regelkreis (control system)​

Aufgaben Regelkreis​

Proportional-Regler (P-Controller)​

Wahl des Faktors kpk_pkp​​

Begrenzung der ermittelten Geschwindigkeit: constrain()​

Pseudocode​

Links​