Gewichteter Mittelwert (Massenschwerpunkt) für mehrere Bodensensoren

Soll ein Roboter mit nur einem Sensor einer Linien folgen, so lässt sich das nur mit einem Trick realisieren: Der Roboter folgt der Linienkante und nicht der eigentlichen Linie. Stehen aber zwei oder mehr Bodensensoren zur Verfügung, ist es möglich der Linienmitte zu folgen. Außerdem können damit Kreuzungen und Verzweigungen erkannt werden oder es kann auf einem gezeichnetten Gitter navigiert werden.

Gewichteter Mittelwert

Bevor verschiedene Algorithmen zum Linienfolgen untersucht werden, ist es notwendig aus den Messwerten der einzelnen Bodensensoren einen einzelnen Wert zu berechnen. Dieser Wert soll die relative Position des Roboters zur Linienmitte angeben. Dies wird, wie bei der Bestimmung des Massenschwerpunkts auf einem Stab, mit dem gewichteten Mittelwert gemacht.

Massenschwerpunkt

Für den Massenschwerpunkt $x_\text{S}$ eines idealen Stabes mit den Massen $m_0$ , $m_1$ , ... an den Stellen $x_0$ , $x_1$ , ... gilt:

x_\text{S} = \frac{ m_0\cdot x_0 + m_1\cdot x_1 + m_2 \cdot x_2 +\cdots + m_\text{n}\cdot x_\text{n}}{ m_0 + m_1 + m_2 + \cdots + m_\text{n}}.

Beispiele für den Massenschwerpunkt eines Stabes

Werden an einem Stab von einem Meter Länge zwei Gewichte $m_0$ und $m_1$ mit einer Masse von jeweils 1 kg befestigt, so ist der Massenschwerpunkt des Stabes intuitiv genau in der Mitte bei 0,5 m.

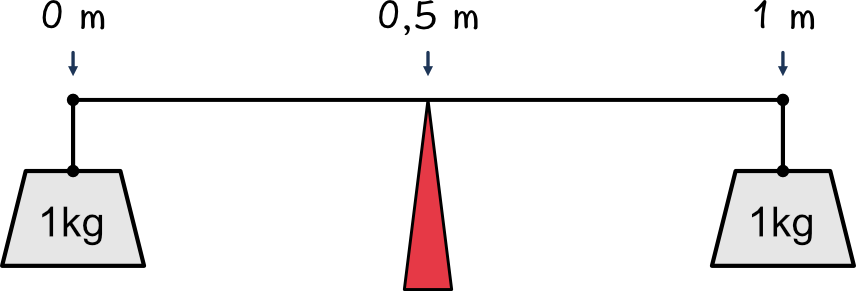
Wird die obige Gleichung verwendet, bestätigt sich die Intuition:

x_\textsf{S} = \frac{ 1 \text{ kg} \cdot 0 \text{ m} + 1 \text{ kg} \cdot 1 \text{ m}}{ 2 \text{ kg}}= 0.5 \text{ m}

Wird das Gewicht am Ende des Stabes auf zwei Kilogramm erhöht, lässt sich vermuten, dass der Massenschwerpunkt bei $2/3$ Meter liegt.

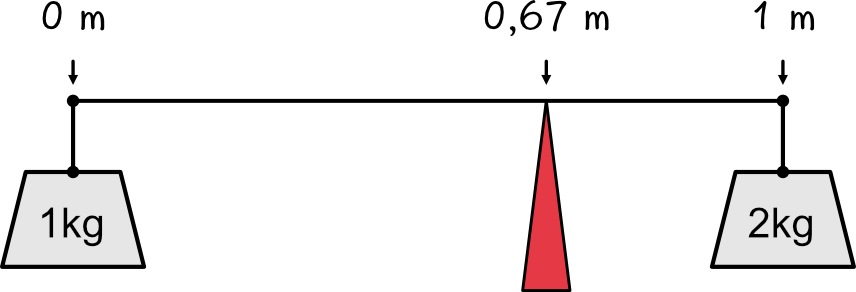
Diese Vermutung wird von der Gleichung ebenfalls bestätigt:

x_\textsf{S} = \frac{ 1 \text{ kg} \cdot 0 \text{ m} + 2 \text{ kg} \cdot 1 \text{ m}}{ 3 \text{ kg}}\approx 0.67 \text{ m}

Im letzten Beispiel wird eine weitere Masse von 1 Kilogramm bei $1/3$ Metern platziert.

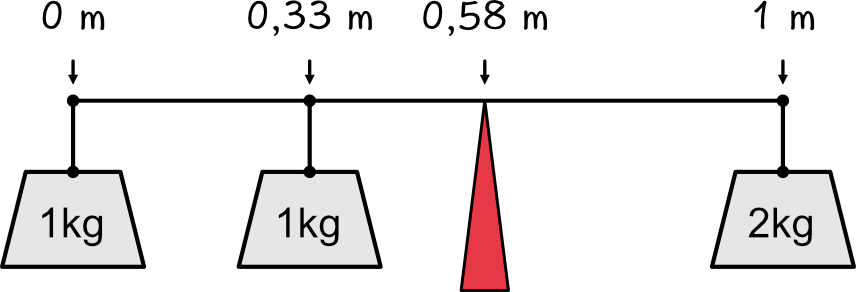
Für diesen Fall kann nur noch mit der Gleichung der richtige Wert für den Massenschwerpunkt ermittelt werden:

x_\textsf{S} = \frac{ 1 \text{ kg} \cdot 0 \text{ m} + 1 \text{ kg} \cdot 0.33 \text{ m} + 2 \text{ kg} \cdot 1 \text{ m}}{ 4 \text{ kg}}\approx 0.58 \text{ m}

Linienposition als gewichteten Mittelwert bestimmen

Zur Bestimmung der Linienposition wird ähnlich vorgegangen wie bei der Bestimmung des Massenschwerpunktes. Da es sich jedoch nicht um Massen, sondern um Sensorwerte handelt, muss die Gleichung ein wenig angepasst werden. Die verwendete verallgemeinerte Formel wird auch gewichteter Mittelwert genannt, da einzelne Werte mit Faktoren gewichtet werden und dann der Mittelwert gebildet wird.

Anstelle der Position der Massen ( $x_0$ , $x_1$ , usw.) werden nun beliebige Gewichtungsfaktoren ( $w_0$ , $w_1$ , usw.) verwendet und die Massen ( $m_0$ , $m_1$ , usw.) werden durch die Sensorwerte ( $S_0$ , $S_1$ , usw.) ersetzt.

P = \frac{w_0\cdot S_0 + w_1\cdot S_1 + w_2 \cdot S_2 +\cdots}{S_0 + S_1 + S_2 + \cdots}

Diese Gleichung bestimmt an welcher Position $P$ sich die Linie relativ zu den Sensoren befindet.

3pi+ / Zumo32u4

Bei den Pololu Robotern 3pi+ 32u4+ oder Zumo 32u4 wurden als Gewichtungsfaktoren die Werte $w_0=0$ , $w_1=1000$ , $w_2=2000$ , usw. gewählt. In der Konfiguration für nur 3 Bodensensoren (nur beim Zumo möglich) ergibt sich somit folgende Gleichung zur Bestimmung der Linienposition:

P _3= \frac{0\cdot S_0 + 1000\cdot S_1 + 2000 \cdot S_2}{S_0 + S_1 + S_2 }

In der folgenden Abbildung ist exemplarisch dargestellt, welche Werte der gewichtete Mittelwert bei entsprechender Position der Sensoren über der Linie annehmen wird.

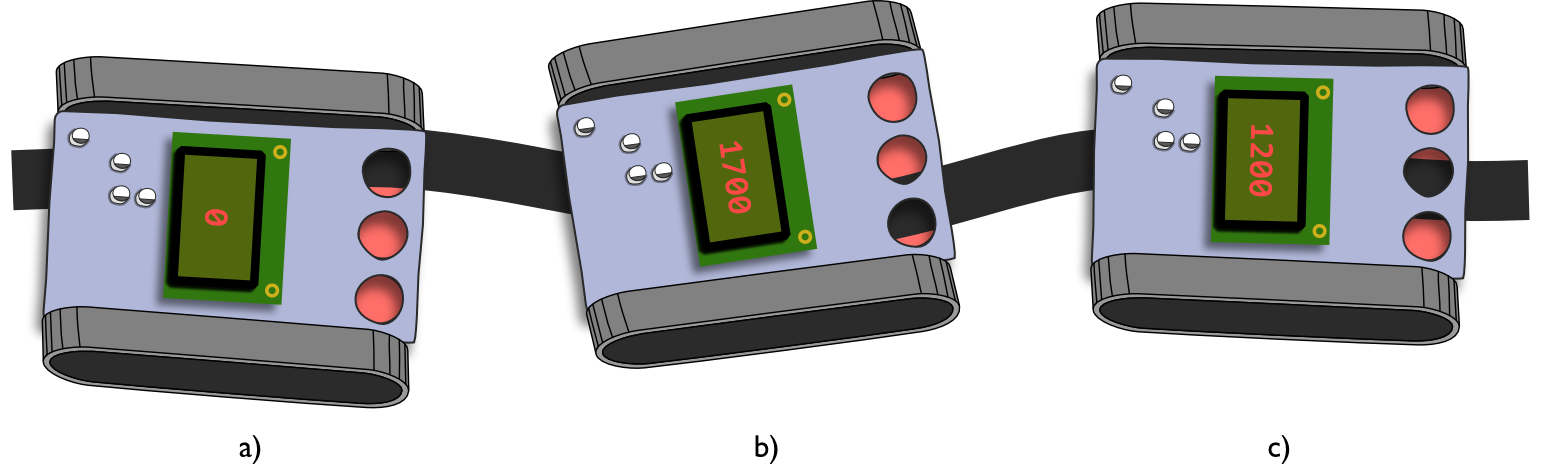
In den Pololu-Bibliotheken für den 3pi+ und den Zumo gibt es die folgenden Befehle zum Auslesen der relativen Linienposition nach dem oben beschriebenen Verfahren des gewichteten Mittelwertes:

3pi+
Zumo

#define NUM_SENSORS 5
sensors lineSensors;                                     // Liniensensor-Objekt

unsigned int lineSensorValues[NUM_SENSORS];              // Array der Sensorwerte
int position = sensors.readLineBlack(lineSensorValues);  // Linienposition

#define NUM_SENSORS 5
Zumo32U4LineSensors sensors;                        // Liniensensor-Objekt

unsigned int lineSensorValues[NUM_SENSORS];        // Array der Sensorwerte
int position = sensors.readLine(lineSensorValues); // Linienposition

Aufgaben

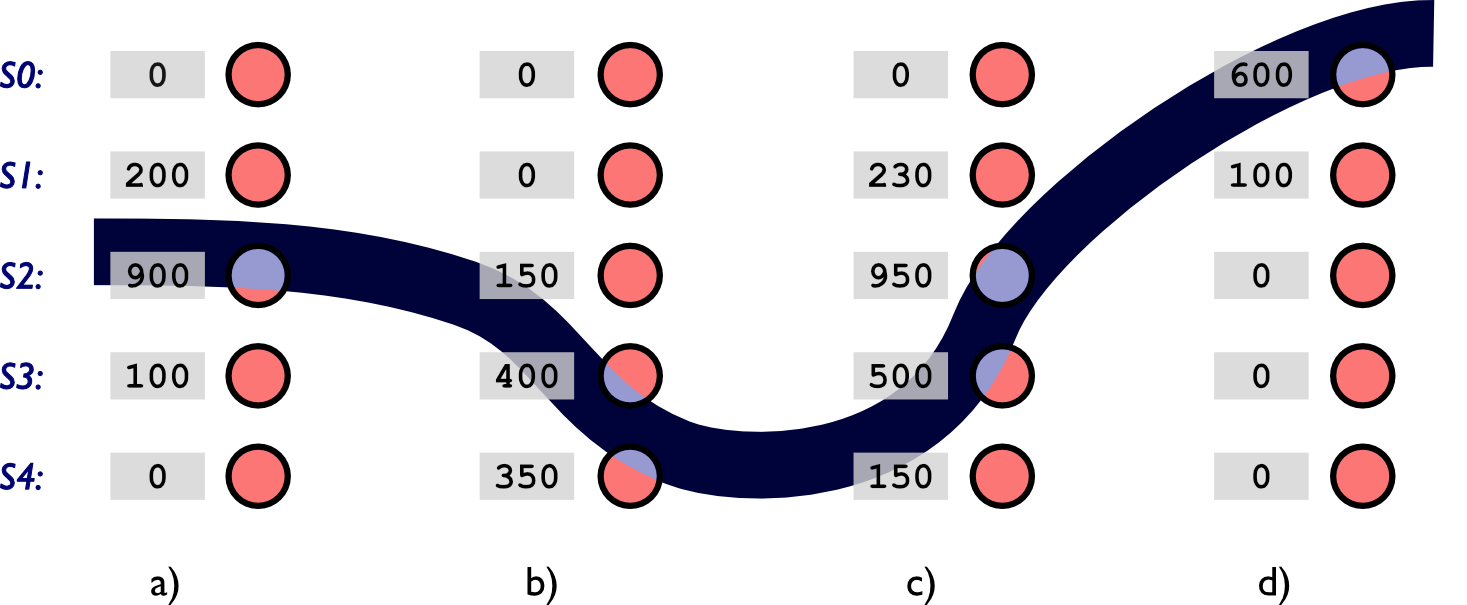
Beispiel für den gewichteten Schwerpunkt mit 5 Sensoren

Berechnen Sie für einen Roboter mit fünf Bodensensoren den gewichteten Mittelwert $P_5$ für die in der Abbildung dargestellten Sensorwerte. Verwenden Sie die oben genannten Gewichtungsfaktoren.
Bei welchem Wert für $P_5$ befindet sich die Linie genau unter dem Sensor S2?
Wo kann sich die Linie befinden, wenn das Ergebnis $P_5=0$ ist?
Wo kann sich die Linie befinden, wenn das Ergebnis $P_5=4000$ ist?
Übertragen Sie das Beispielprogramm für die Liniensensoren auf ihren Pololu Roboter. Das Programm gibt als gewichteten Mittelwert die Linienposition mit Werten zwischen 0 und 4000 (2000 mittig über der Linie) auf dem Display aus.
Analysieren Sie, welche Werte für welchen Versatz ausgegeben werden und vergleichen Sie diese mit den Aufgaben 1. bis 4. Welchen Einfluss hat die Linienbreite auf das Ergebnis?