Linienfolger mit einem PD-Regler

Für den Kantenfolger wurde der einfache, aber dennoch effiziente P-Regler zum Folgen der Kanten verwendet. Der P-Regler funktioniert mit dem richtigen Proportionalitätsfaktor $k_p$ in der Regel sehr zuverlässig. Trotzdem neigt er aber zu starken Oszillationsbewegungen, d.h. er wackelt an der Kante entlang, anstatt dieser ruhig zu folgen. Der sogenannte PD-Regler verbessert das Fahrverhalten des Linienfolgers besonders bei hoher Geschwindigkeit deutlich.

Pseudocode P-Regler (Linienfolger)

Bevor im Folgenden schrittweise der PD-Regler eingeführt wird, wird noch einmal kurz der Pseudocode des P-Reglers für einen Linienfolger erläutert.

// Linienfolger        

wertLinie = 500                           // Sollwert Linienkante
kp        = 0.1                           // Proportional-Faktor
MSPEED    = 100                           // mittlere Motorgeschwindigkeit


wiederhole
    wertSensor = messenIrSensor()         // Wert zwischen  0 und 1000
    error      = wertLinie - wertSensor   // Fehlerwert (Regeldifferenz)
    deltaSpeed = error * kp               // P-Regler - Ändert die Geschwindigkeit
    leftSpeed  = MSPEED - deltaSpeed      // Drehzahl links bestimmen
    rightSpeed = MSPEED + deltaSpeed      // Drehzahl rechts bestimmen

    begrenze(leftSpeed)                   // Drehzahl auf sinnvolle Werte begrenzen
    begrenze(rightSpeed)                  // (beim Zumo zwischen -400 und +400)
    setSpeeds(leftSpeed,rightSpeed)       // Aktualisieren der Motordrehzahlen  

Bei einem P-Regler hängt die Stellgröße proportional vom Fehler, also der Regelabweichung ab. Ist der Roboter weit von der Linie entfernt (große Regelabweichung), soll er stärker in Richtung Linie lenken, als wenn die Regelabweichung geringer ist. Damit der Roboter auch bei höheren Geschwindigkeiten engen Kurven gut folgen kann, muss der Proportionalitätsfaktor relativ groß gewählt werden. Dass kann jedoch dazu führen, dass der Roboter anfängt zu oszillieren, also an der Linie entlang wackelt, anstatt dieser geschmeidig zu folgen.

Mit dem Differential-Anteil eines Regler ist es mögliche diese overshoots oder Oszillationsbewegungen zu reduzieren, und den Roboter trotzdem sehr schnell auf Änderungen reagieren zu lassen.

Differential-Anteil

Bei einem Regler mit Proportional- und Differential-Anteil (PD-Regler genannt) werden beide Anteile entsprechend ihrer Gewichtungsfaktoren ($k_p, \, k_d$) addiert.

Wie kann nun mit dem Differential-Anteil das Oszillieren durch einen zu großen Proportional-Anteil reduziert werden? Schauen wir uns dazu den ersten Fall in der folgenden Grafik an: Fehler wird kleiner. In diesem Fall fällt der Fehler (also die Abweichung des Roboters von der Linie) linear. Da der Proportional-Anteil aber zu groß ist, wird der Roboter nicht über der Linie bleiben, sondern unter anderem wegen der Trägheit über das Optimum (Linie) hinwegfahren.

Der Differentialanteil wird aus dem Anstieg bzw. Änderung des Fehlers bestimmt. Da der Fehler fällt, ist der Anstieg negativ und der D-Anteil liegt somit unter null. Der Stellwert, also DeltaSpeed wird aus der Summe vom Proportional- und Differentialanteil berechnet, weshalb der Differentialanteil in diesem Fall der Lenkbewegung zur Linie entgegenwirkt. Er reduziert also das Überschwingen.

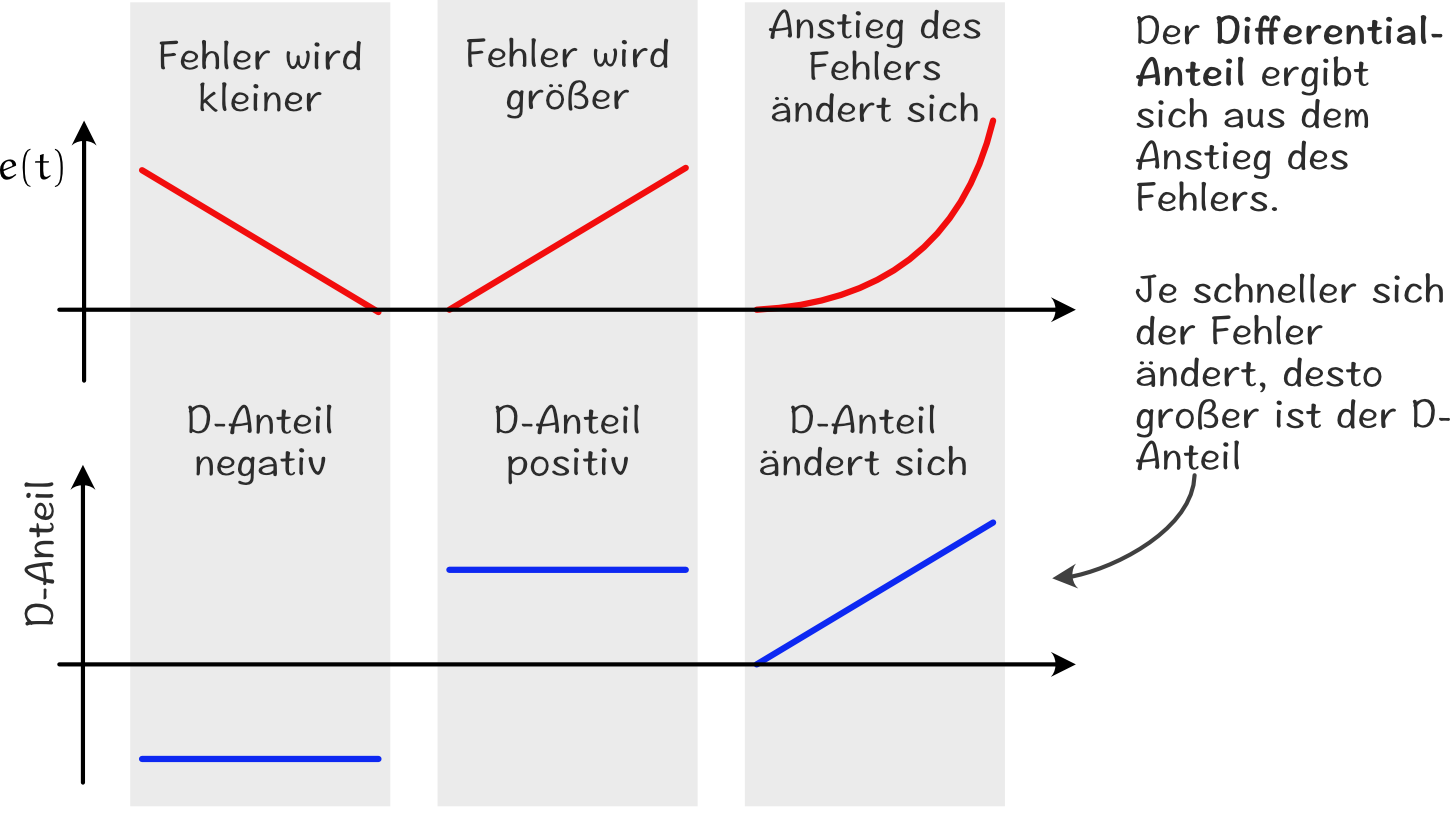
Nehmen wir ein anderes Beispiel. Der Roboter folgt perfekt einer Linie. Der Fehler ist sehr klein und der Regler funktioniert problemlos. Plötzlich erreicht der Roboter eine sehr scharfe Kurve. Der Fehler wäre anfangs noch moderat, würde dann aber, weil der Roboter nicht schnell genug lenkt, sehr stark ansteigen, also einen großen Anstieg aufweisen. Dieser positive Anstieg des Fehlers (Fehler wird größer) verursacht einen positiven Differentialanteil, was die Lenkbewegung verstärkt und hilft der Kurve besser zu folgen.

Im letzten Beispiel Anstieg des Fehler ändert sich ändert sie der Fehler nicht gleichmäßig, sondern der Anstieg wird mit der Zeit immer größer. In diesem Fall ändert sich auch der Differentialanteil, er wird größer und versucht der Änderung entgegenzuwirken.

Berechnen des Differential-Anteil

Mathematisch entspricht der Differential-Anteil der 1. Ableitungen des Fehlers. Alternativ, und mit dem Arduino viel einfacher zu bestimmen, kann der Differenzenquotient des Fehler berechnet werden. Für den Differenzenquotient gilt:

$$m = \frac{y_1-y_0}{x_1-x_0}.$$

Wird diese Gleichung auf den Fehler $e$ angewendet, ergibt sich ein einfacher Ausdrück für den Anstieg, bzw. die Änderung des Fehler $e'$, also den gesuchten Differentialanteil differential des Reglers:

$$e' = \frac{e_\text{neu}-e_\text{alt}}{t_\text{neu} - t_\text{alt}} = \frac{e_\text{neu}-e_\text{alt}}{\Delta t}.$$

Der Pseudocode für den Differential-Anteil könnte wie folgt aussehen:

differential = (error - error_alt) / dTime

Wenn das Zeitintervall dTime zwischen den Messerwerten immer gleich ist (oder zumindest sehr ähnlich), kann auf die Multiplikation mit dTime verzichtet werden. Dadurch ergibt sich für den D-Anteil eine einfache Subtraktion.

differential = error - error_alt

Der Erweiterte PD-Regler ergibt sich nun aus dem mit $k_p$ und $k_d$ gewichteten P-Anteil und D-Anteil:

differential = error - error_alt               // Differential-Anteil
deltaSpeed   = error * kp + differential * kd  // PD-Regler mit den Faktoren 
                                               // kp (proportional) und
                                               // kd (differential)

Pseudocode PD-Regler

Für den vollständige Pseudocode des PD-Reglers (Proportional-Differential-Reglers) wird von konstanten Zeitintervallen zwischen den Messungen ausgegangen und der dTime Term vernachlässigt.

// Kantenfolger mit einem Sensor        

wertLinie     = 500             // Sollwert (Sensorwert genau über der Linie)
kp            = 0.2             // Proportional-Faktor
kd            = 1               // Differential-Faktor
MSPEED        = 100             // mittlere Motorgeschwindigkeit

wiederhole
    wertSensor   = messenIrSensor()        // Wert zwischen  0 und 4000
    error        = wertLinie - wertSensor  // Fehlerwert, Regelabweichung
    differential = error - error_alt       // Differential-Anteil

    error_alt  = error                     // den letzten Fehler speichern
                           
    deltaSpeed = error * kp  + differential * kd // PD-Regler   
                                
    leftSpeed  = MSPEED - deltaSpeed       // Drehzahl links bestimmen
    rightSpeed = MSPEED + deltaSpeed       // Drehzahl rechts bestimmen

    begrenze(leftSpeed)                    // auf sinnvolle Werte begrenzen
    begrenze(rightSpeed)
    setMotors(leftSpeed,rightSpeed)        // Aktualisieren der Motordrehzahlen

Aufgaben

1. Programmieren Sie einen Linienfolger mit PD-Regler.
   1. Implementieren Sie den PD-Regler mit einem änderbaren D-Faktor. Nutzen Sie zum Ändern des D-Faktors kd zwei Tasten auf dem Roboter. Der aktuelle kd-Wert sollte auf dem Display angezeigt werden.
   2. Untersuchen sie zuerst den Einfluss des D-Anteils (mit konstantem P-Faktor). Ab welchem Wert beeinflusst der D-Anteil das Verhalten des Roboters. Wie verhält sich der Roboter, wenn der D-Anteil zu größ wird. Versuchen Sie das Verhalten zu erklären.
   3. Erhöhen Sie die Motorgeschwindigkeit. Mit welcher Maximalgeschwindigkeit kann der Roboter noch der Linie folgen?
2. Lassen Sie Ihre Linienfolger gegeneinander antreten. Welcher Roboter folgt der Linie am schnellsten?

Einstellen der Parameter kp und kd

Das Konfigurieren der Parameter für den PD-Regler erfordert Geduld und Übung. Die folgenden Hinweise sollen helfen, die Parameter für eine Strecke mit unterschiedlichen Kurvenradien anzupassen.

1. Alle Faktoren auf Null setzen. Roboter mit geringer Geschwindigkeit fahren lassen.
2. Den P-Faktor erhöhen, bis der Roboter einer geraden Strecke problemlos folgen kann und Kurven mit großen Radien mit leichten Schwingungen folgt.
3. Erhöhen des D-Faktors, bis die Oszillationen verschwinden.
4. Schritte 2 und 3 wiederholen, bis eine Erhöhung des D-Faktors die Oszillation nicht mehr verschwinden lässt. (Bei zu großem D-Anteil wird der Roboter aufgrund von Rauschen anfangen zu zittern)
5. P und D-Faktoren auf den letzten stabilen Wert setzen.

In der Regel sollte der Roboter nur sehr wenig oszillieren. Jedoch kann ein geringes Oszillieren auch bedeuten, dass der Roboter engen Kurven nicht immer perfekt folgen kann.

Mögliche Erweiterungen des PD-Reglers

• PID-Regler mit Integralanteil
• Geschwindigkeit bei großen Fehlern verringern
• Zeitdifferenz zwischen den Messwerten berücksichtigen
• Tiefpassfilter für das Sensorsignal zum Verringern des Rauschens

Links

• PID-Simulator
• PID without a PhD
• PID Balance+Ball | full explanation & tuning
• Großartige Videoreihe zum PID-Regler. Es gibt kaum besser Videos zum Thema: Understanding PID Control